Sześć ostrzeżeń i jednocześnie sześć alternatyw – przedstawia Youki Terada. Autor znany mi jest z bardzo dobrych artykułów, a ten artykuł jeszcze bardziej mi pasuje, jako nauczycielce matematyki. bo też nauczałam matematyki
Tym razem Terada zajął się nauczaniem podstaw matematyki. Ale myślę, że jego sześć ostrzeżeń przyda się wszystkim nauczycielom matematyki, a może też innych przedmiotów.
Jego zdaniem dużo nacisku w nauczaniu matematyki kładzie się na podstawowe pojęcia związane z dodawaniem, mnożeniem, odejmowaniem i ułamkami. Przy czym najważniejsze jest osiągnięcie sprawności liczenia, szybkości i podawania właściwej odpowiedzi. Oczywiście biegłość ma duże znaczenie, ale według badaczki Giny Kling ćwiczenie tych umiejętności nie powinno odbywać się kosztem rozumowania matematycznego i znajomości i zrozumienia procedur. Jennifer i Bay-Williams sugerują na podstawie swoich badań z 2021 roku, że wiele powszechnych praktyk nauczycielskich pokazuje uczniom, że matematyka dla ucznia polega zasadniczo na przypominaniu i ślepym przestrzeganiu formuł. Zamiast tego powinniśmy ożywiać matematykę, poprzez projektowanie takich doświadczeń uczniowskich, które kładą nacisk na ciekawość, elastyczność i zadziwienie i promować matematykę jako potężne narzędzie do rozumienia świata.
Kling i Bay-Williams twierdzą, że metody, które można nazwać „szybkimi naprawami”, faktycznie utrudniają uczenie się matematyki. Ich zdaniem poświęcanie czasu na krótkie zadania i skupianie się na szybkości i zapamiętywaniu (badania z 2013 roku) może wywoływać u uczniów niepokój i chęć unikania matematyki, już nawet w pierwszych latach uczęszczania do szkoły.
Oto sześć bezproduktywnych praktyk matematycznych, których nauczyciele powinni unikać.
- IGNOROWANIE STRATEGII WIZUALIZACJI
Błędne jest założenie, że można werbalnie wyjaśnić uczniom strategię matematyczną. Nauczyciele nie mogą liczyć na to, że uczniowie coś zrozumieją, kiedy zostanie im to tylko powiedziane. Uczniowie potrzebują czasu i doświadczenia, aby coś zrozumieć i zwizualizować.
Terada proponuje zastosowanie kart Quick Look , polegających na pokazywaniu kart z różną liczbą kropek lub zdjęć znanych przedmiotów, a następnie zapytanie uczniów ile widzieli i jak je widzieli. Na przykład, czy widzieli cztery grupy po dwie lub dwie grupy po cztery? Taka wizualizacja może pomóc uczniom lepiej zrozumieć, jak i dlaczego działają strategie matematyczne, w tym przypadku – mnożenia. Jest to spojrzenie na tę samą rzeczywistość z różnych stron.
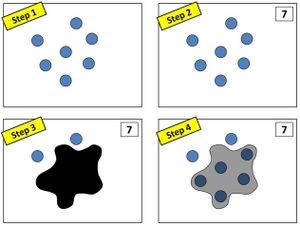
Steve Wyborneya proponuje inna grę – Splat! . Na slajdzie pokazuje uczniom zestawy kropek, prosi uczniów o ich przeliczenie, następnie pokazuje następny slajd, na którym część kropek jest ukryta. Zadaniem uczniów jest policzenie ile kropek zostało ukrytych. Poniżej przykład kart do tej gry. Uczniowie sami znajdują sposób wyliczenia.
©Steve Wyborney
- NAUCZANIE W KOLEJNOŚCI NUMERYCZNEJ
Powszechnym podejściem jest nauczenie dodawania i mnożenia w kolejności wzrastającej, czyli od zer, przechodząc do jedynek, a następnie dwójek i trójek. Dzieje się tak zwykle przy nauce tabliczki mnożenia. Niestety wtedy uczniowie postrzegają matematyczne operacje, jako osobne strategie, co ostatecznie obniża poziom osiągnięć ucznia.
Lepiej zacząć od np. 2, 10 i 5. Po pierwsze operujemy na bardziej znanych i „używanych” liczbach, ale również można z poznanych sposobów wyprowadzić strategie na mnożenie przez inne liczby. Na przykład, gdy uczeń nauczy się mnożenie przez 2 i 5, może rozłożyć trudny problem: 8 x 7 – na 8 x 5 plus 8 x 2, albo podobnie zrobić w przypadku trudniejszym –
56 x 8.
Następnie warto przejść do mnożenie liczby przez siebie samą (np.: 7 x 7), a to dlatego, że niektóre z najtrudniejszych iloczynów (np. 7 × 8 i 6 × 7) są zbliżone do mnożenie tych samych liczb przez siebie. Trzeba też mieć na względzie, że kwadraty są przydatne w późniejszej pracy z algebrą, geometrią i pomiarami.
- TRZYMANIE SIĘ JEDNEGO SPOSOBU ROZWIĄZYWANIA PROBLEMu
Kiedy uczniowie po raz pierwszy uczą się odejmowania, często wykorzystują dodawanie. Na przykład, jeśli mają obliczyć 15 – 9, zastanawiają się – ile trzeba dodać do 9, aby otrzymać 15. To dobre podejście, ale to tylko jedna strategia z wielu i nie trzeba ignorować innych, bo to może hamować zdolność ucznia do rozwiązywania bogatszych problemów.
Lepiej poprosić uczniów, aby pomyśleli o różnych strategiach — na przykład zamieniając 15-9 na 15-10, a następnie dodając 1 do odpowiedzi. Uczniowie powinni również nauczyć się, jak odróżniać to, od czego odejmujemy, od tego – co odejmujemy. Na przykład w zadaniu 15-9 można rozdzielić 15 na 10 i 5 i pokazać uczniom, że mogą najpierw obliczyć 10-9, a następnie dodać 5. Gdy uczniowie nauczą się różnych strategii, to mogą przejść do trudniejszych problemów, takich jak: 132–99 (132–100 = 32, a następnie dodać 1).
Stosowanie wielu strategii pokazuje sens poszukiwań i dążenia do najlepszego sposobu rozwiązania.
- SKUPIANIE SIĘ NA OPANOWANIU FAKTÓW I ICH PRZYPOMINANIU
Skupianie się na rozwiązywaniu z uczniami wielu zadań, uczy ich, że szybkość i mechaniczna biegłość są ważniejsze niż rozwijanie zrozumienia matematyki. Rozwiązywanie wielu podobnych problemów nudzi uczniów, skłania wielu z nich do opinii, że nie lubią matematyki.
Podobnie jest z uczeniem się i zapamiętywaniem procedur i sztuczek, np. szybki sposób na mnożenie przez 9 przy pomocy palców, nie pomaga w innych przypadkach. Chociaż może to być przydatny punkt wyjścia, lepiej jest pomóc uczniom, ucząc ich strategii rozumowania. Weźmy przykład dodawania: 69 + 58, może wydawać się trudne, ale jeśli uczniowie dodadzą 1 do 69 i odejmą 1 od 58, to przekształcą problem w łatwiejszy: 70 + 57. To pomaga uczniom nauczyć się płynnie manipulować liczbami.
Autor proponuje również skorzystać z praktycznych gier i interaktywnych zajęć: gry matematyczne, takie jak dodawanie bingo i łączenie czterech , one pokazują, jak dobrze uczniowie czują się w stosowaniu różnych strategii matematycznych – takich jak dzielenie liczb i szacowanie – oraz uzasadnienie odpowiedzi. To może znacznie zwiększyć zamiłowanie uczniów do matematyki.
- ZBYT DUŻY NACISK NA SZYBKOŚĆ
Konkursy szybkości, takie jak wyścigi planszowe i gry na czas, są zabawne i mogą pomóc młodym uczniom ćwiczyć szybkie dodawanie, odejmowanie i mnożenie — ale, nie należy z nimi przesadzać.
Zbyt wczesne docenianie szybkości, zdaniem Kling i Bay-Williams, może przeszkadzać w osiągnięciu płynności. Jeśli cenimy szybkość, to zachęcamy uczniów do stosowania prostych strategii, zamiast ćwiczenia bardziej złożonych, czasochłonnych strategii. które budują elastyczne umiejętności rozumowania matematycznego.
Autor zaleca grę Tens Go Fish, w której gracze szukają kombinacji dwóch kart, które sumują się do 10. Jeśli uczeń ma w ręku 7, może poprosić przeciwnika o 3.
- stosowanie TESTów na CZAS
Wymóg czasowy zmniejsza płynność matematyczną. Chociaż testy czasowe mogą czasami służyć do szybkiej oceny płynności, są słabym sposobem mierzenia umiejętności myślenia. Za to wywoływują niepokój, hamują jasne myślenie, karzą uczniów, którzy podchodzą do zadań analitycznie i wzmacniają opinię, że matematyka jest ponurą, bezlitosną dyscypliną.
Zamiast tego warto wprowadzać w pracy z uczniami strategie:
- Dzielenia się opiniami i refleksją w parach – dzielenie się
- Przeprowadzanie wywiadów z innym uczniem – wywiady rówieśnicze
- Prowadzenie dziennika przez ucznia – dziennika,
- Zadawanie uczniom pytań otwartych – pytania otwarte
- Przekazywanie uczniom wiedzy na kanwie historii opowiadanie historii
Ale najważniejsze jest pytanie kierowane do ucznia: „jak do tego doszedłeś w miejsce pytania o wynik.
Link do artykułu: