No, to jest długa i skomplikowana historia. Ale przynajmniej ładna. Warto ją poznać m.in. dlatego, że nie da się tych rzeczy dowiedzieć z Wikipedii, choć jest tam sporo, ani – o ile wiem – z żadnego podręcznika. Będzie trudno, bo to szkoła, a nie uniwersytet pedagogiczny i trzeba będzie nie tylko przeczytać ten potok słów poniżej, ale również samemu myśleć, rysować, bawić się komputerowymi symulacjami. Bez tego się nie da.

Uwaga, to nie jest materiał dla dzieci, o czym przypominam raz jeszcze. Nie jest to jednak tym razem również propozycja lekcji, czy nawet zawartości programowej. Bez wątpliwości żadne dziecko w szkole podstawowej nie wytrzyma tak długotrwałego skupienia, jak tego wymaga poniższe. Zagadnienie należy do najtrudniejszych wyzwań dla matematycznej wyobraźni, a jednak nie wymaga żadnego innego przygotowania, poza tym zawartym tu w poprzednich częściach niejako przy okazji nauki o liczbach i dziesiętnym systemie. Skoro zaś mowa tu o wyobraźni, to może się okazać, że to jest jeden z tych przypadków, kiedy dzieci radzą sobie lepiej niż dorośli.

W przedszkolach i szkołach Montessori dzieci widzą liczby od 1 do 10 w postaci połączonych ze sobą w rodzaj sznurka paciorków. 10 takich sznurków przyczepionych jeden obok drugiego tworzy kwadratową setkę. 10 setek ułożonych jedna nad drugą w przestrzenną kostkę tworzy tysiąc. U progu szkoły dzieci Montessori mają bardzo dobrą świadomość liczb, potrafią „liczyć ze zrozumieniem” natury systemu dziesiętnego, a stosowane w podstawie programowej „zakresy” (do 10, do 30, do 100 itd.) nie mają dla nich żadnego znaczenia.

No dobrze, ale jak wyobrazić sobie 10 tysięcy? To pytanie chciałbym postawić przed dziećmi, ewentualnie dopowiadając doń jedną lub dwie historyjki. Niniejsze jest po to, by zadający pytanie dorosły był z kolei przygotowany na pytania dzieci. I by nie musiał odpowiadać, że zrozumieją, kiedy dorosną.

Odpowiadać na zaczepkę o tysiące można na wiele sposobów, ale pytamy tu oczywiście o ten zgodny z dotychczasową logiką układania paciorków. To zaś wymaga czwartego wymiaru przestrzeni i podróż w tę stronę jest przedmiotem niniejszego. Czy da się pobawić z małymi dziećmi tak, żeby potrafiły myśleć nie tylko przestrzennie, ale właśnie hiperprzestrzennie ponad ograniczenia widzialnego świata i tej przestrzeni, której nie musimy sobie wyobrażać, bo ją po prostu widzimy?

W odróżnieniu od poprzednich części niniejszego, które dość dobrze sprawdziłem z dziećmi ze szkół podstawowych i wiem, że „działają”, tego jeszcze sprawdzić nie zdołałem. Mówiąc otwarcie, nie mam pojęcia, czy to się może udać, choć sądzę, że tak. Co więcej, wydaje mi się to naturalnym zwieńczeniem zarówno zabaw i problemów tu opisanych, jak i tych jeszcze tu brakujących, a dotyczących geometrii. Czemuś w końcu służą te wprawki w widzeniu rzeczy, jakimi one są w swojej najgłębszej strukturze.

Trening w nadprzestrzeni jest oczywiście treningiem w myśleniu i to jest jedna z jego podstawowych zalet. Ale, wracając do pytań – przede wszystkim ważne są te wszystkie pytania o to, w jakim naprawdę świecie żyjemy. Są dotąd nierozstrzygnięte i są z wysiłkiem rozważane w nauce. Czteroprzestrzeń Einsteina-Minkowskiego okazała się istnieć w zdumiewający sposób realnie, a nie jest tylko modelem pozwalającym poradzić sobie z rozmaitymi aberracjami obserwacyjnymi wynikającymi z ograniczeń percepcji. Wiele zjawisk kwantowych sugeruje, że modele matematyczne mają własną realność, twardszą nierzadko niż samo istnienie opisywanej nimi materii i przestrzeni. Wiele faktów przemawia za tym, że istniejemy w rzeczywistości o zdecydowanie więcej niż trzech wymiarach, o których wydaje nam się, że je widzimy. Mówimy tu o nowych i nierzadko szczytowych osiągnięciach nauki – ja jednak nie widzę powodu, by dzieci nie miały ich poznać w ramach kształcenia ogólnego, choćby na popularnym poziomie. Feynmana wykład elektrodynamiki kwantowej dla laików jest równocześnie prawdziwy i rzeczywiście zrozumiały – zrozumieć są go w stanie również dzieci, dlaczego więc koniecznie mamy je zamiast tego katować prawem Ohma, z którego prosty jest zresztą wyłącznie sam wzór, natomiast natura zjawiska pozostaje nieznana, a w dodatku w sporym stopniu po prostu zafałszowana szkolnym wykładem?

Platon i Dali zostali na wstępie przywołani właśnie w kontekście pytania o rzeczywistą naturę i „kształt” świata. W Dialogach kajdany opisano jako przyrodzoną być może kondycję człowieka. Trzeba by je zerwać, wyzwolić więźnia, wyprowadzić go z jaskini na pełne światło dnia, niechby i nawet przemocą, byleby raz zobaczył rzeczy w ich właściwej naturze. Być kimś wyzwolonym w ten sposób, to może nawet nie być już człowiekiem – ale kimś już „spoza tego świata”, z jakiegoś świata innego, z jakiejś „światłości” być może. Dali w jakimś sensie pokazuje moim zdaniem właśnie taką perspektywę, co spróbujemy tu wyjaśnić, ale tymczasem – jeśli mi wolno dyskutować z Platonem, którego fragment o jaskini porusza mnie nieodmiennie i niezależnie od tego, ile go razy czytam – zwróćmy uwagę, że więźniowie jaskini nie są wcale bez szans nawet pozostając w kajdanach. Bo cienie wiele mówią o naturze rzeczy, od których pochodzą. Jeśli uważnie patrzeć. I myśleć. Myślenie i wyobraźnia mają moc zrywania łańcuchów.

Zróbmy to więc.

Niestety jest to proces wymagający wysiłku. Bywają w matematyce momenty stosunkowo łatwo osiągalnych „widzeń”, kiedy zaczynamy rozumieć nagle rzeczy dotąd nam niedostępne. Hiperprzestrzeń – przynajmniej dla mnie – wymaga jednak poznawania systematycznego, a co gorsza, kiedy już umiemy sobie wyobrazić jedną hiperbryłę, poznawanie drugiej będzie co prawda łatwiejsze, ale wcale nie natychmiastowe.

Jaki jest powód, by zadać sobie taki wysiłek? Wysiłek jest niemały, więc i powód trzeba mieć do tego dobry. Cóż, z całą pewnością każdy musi odnaleźć powód własny, ale istnieje też powód wspólny dla wszystkich i on jest właściwy dla matematycznego poznania, które bywa źródłem euforii nieznanej innym rodzajom aktywności. Wspomniane pytania o rzeczywisty kształt świata są jak najbardziej naukowe i jeśli kogoś interesuje odpowiedź – niech się z tym zagadnieniem zmierzy. Rozmaite tunele czasoprzestrzenne, mniej lub bardziej spójne popularnonaukowe lub czysto fikcyjne konstrukcje, teleportacja dla przykładu – jak to mogłoby być możliwe? To są te właśnie klasy zagadnień i dotyczą one również konkretnej rzeczywistości laboratoriów naukowych z kwantową bilokacją i podobnymi dobrze zbadanymi, choć bynajmniej nie zrozumianymi zjawiskami. Wielowymiarowe przestrzenie mają też dzisiaj wiele zastosowań technicznych. Silne procesory komputerów budowano na modelu sześcianu w czterech wymiarach zwanego tesseraktem, który tu będziemy poznawać – dokładnie tego samego, którego specyficzną postać namalował Salvador Dali w swym Ukrzyżowaniu, nadając mu sens metafizyczny, choć moim zdaniem najzupełniej rzeczywisty. Wiele technicznych, wręcz mechanicznych problemów przedstawia się i rozwiązuje w wielowymiarowych przestrzeniach. Ale hiperprzestrzeń ma również znaczenie filozoficzne, jak wspomniane Ukrzyżowanie – i choć do niedawna sam bym o to Dalego nie posądzał, te głębokie idee, które on w swoim obrazie zawarł, choć one dotyczą teologii, a nie logiki, można zrozumieć w pełni raczej jednak tylko wtedy, kiedy się rozumie sens matematycznej idei hiperprzestrzeni. W jej platońskim znaczeniu realności przeciwstawionej iluzji cienia w jaskini. Wreszcie znam więcej niż jedną osobę, która pogrążona w halucynacjach psychiatrycznej natury, zdołała je przezwyciężyć jak Nash w Pięknym umyśle, studiując rzeczywistość właśnie tak wnikliwie, jak tego potrzeba w hiperprzestrzeni i uwalniając się ze strasznych kajdan ciężkiej choroby umysłu na podobieństwo owego platońskiego więźnia, który zrozumiał zachowanie cieni, wiedząc wreszcie, jakie to światło naprawdę je rzuca i w jaki sposób. Każdy z tych wymienionych powodów – naukowy, techniczny, filozoficzny, mistyczny i nawet ów psychiatryczny – prowadzi do wyzwolenia podobnego temu opisanemu przez Platona, a każdy jest przygodą w najpełniejszym znaczeniu. Bo na końcu długiej i żmudnej drogi w końcu czeka nas ów charakterystyczny dla matematycznego poznania moment „WIEM!”, albo też w tym przypadku „WIDZĘ!” To ten moment – całkiem niezależnie od wszelkich możliwych wymienionych tu motywacji – jest wart całego tego wysiłku. Można potem spojrzeć wstecz z tą samą satysfakcją, którą muszą czuć himalaiści patrząc ze zdobytego właśnie szczytu na piękny świat pod nimi.

No, a dzieci…

Dzieciom – jeśli naprawdę koniecznie trzeba traktować je inaczej – można opowiedzieć dowolną historię opartą chociażby na poniższym. Można się odwołać do jakiegoś filmu, w którym pokazuje się „nadprzestrzeń” lub „teleportację” – bo choć to wydaje się niewiarygodne, nawet najgorsze z tych przedstawień zawsze zawierają jakąś prawdę, do której da się nawiązać. Mam nadzieję móc wkrótce zaoferować dzieciom cztero- i więcej wymiarowy labirynt do eksploracji – a w nim moc przygód, jakie dzieci lubią. Ale zawsze warto powtórzyć zadane już tu proste pytanie – jak, na Boga, wygląda kostka dziesięciu tysięcy liczb, skoro tysiąc mieści się w sześcianie?

Często używa się w takich „hiperprzestrzennych okazjach” figury „robaków płaszczaków”, istot dwuwymiarowych, ze swej płaskiej natury niezdolnych nie tylko do postrzegania trzeciego wymiaru przestrzennego, ale również do myśli, że coś takiego może istnieć. Przyjrzyjmy się naprzód ograniczeniom świata płaszczaków i przećwiczmy je na naszym komputerowym modelu. Proszę na razie nie włączać opcji "4D", zostawiając ją sobie na koniec i posługiwać się wyłącznie modelami 3D i 2D. 4D wymaga zrozumienia, które jest treścią niniejszego.

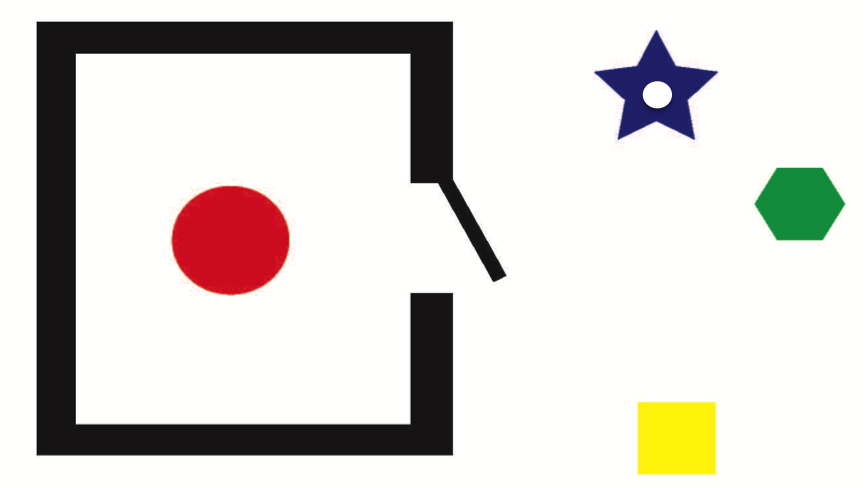
Robaki płaszczaki żyją, jako się rzekło, w kompletnie płaskim świecie. Mogą się poruszać w przód, w tył, w lewo, w prawo i po wszelkich skosach, mogą rozglądać się we wszystkich tych kierunkach, natomiast góra i dół nie istnieją i robaki nie umieją sobie ich w ogóle wyobrazić. Pochodząca z tego świata „czerwona kropka” została umieszczona w celi, drzwi za chwilę się zamkną. Patrzymy na tę scenę z góry, a więc z perspektywy nie tylko niedostępnej płaszczakom, ale również kompletnie dla nich niewyobrażalnej. „Żółty kwadrat” widzi tę scenę następująco (linie mają tu grubość, żebyśmy cokolwiek widzieli – robaki w sobie tylko znany sposób widzą linie nieskończenie cienkie):

Jest niewykluczone, że nasze robaki dysponują parą nieskończenie płaskich oczu i potrafią dzięki nim widzieć obydwa przestrzenne wymiary, widząc głębię i oceniając również odległość. Jeśli nawet nie działa u nich stereoskopia, widzą perspektywę, dostrzegają paralaksę, rozumieją głębię wzdłuż osi własnego wzroku. Przez uchylone drzwi widać fragment „czerwonego więźnia”, seksowna „strażniczka gwiazdka” i gburowaty „zielony sześciokątny klawisz” są oboje widoczni w postaci kresek. Wyposażony w parę oczu kwadrat mógłby docenić kształty powabnej strażniczki – w przeciwnym wypadku musiałby je studiować uważnie obchodząc ją wkoło. My widzimy jej kształt w pełni patrząc z wyżyn niedostępnego płaszczakom trzeciego wymiaru. Byłoby jednak błędem uważać, że żółty, oczarowany powabami strażniczki, byłby w zachwycie, widząc, co widzimy my, czyli pełnię uroków gwiazdeczki z jej wielokrotnie i głęboko wciętą talią. Widzimy bowiem rzeczy, które w świecie płaszczaków wymagałyby techniki zdjęć rentgenowskich i solidnej komputerowej obróbki danych. Patrząc z góry, widzimy coś, co dla obecnych na płaszczyźnie robaków płaszczaków jest ich „wnętrznościami”. Widzimy więc np. białą kropkę wewnątrz gwiazdki – niech nam się nie wydaje, że to jakiś uroczy pieprzyk, nasz kwadrat zobaczyłby tę kropkę wyłącznie na zdjęciach z USG. I raczej nie byłby oczarowany, bo takie zdjęcia rzadko bywają sexy. Z tego punktu widzenia nadprzestrzeń rozczarowuje (choć ekscytowała np. Picassa). Ale są też inne punkty widzenia.

Wyobraźmy więc sobie, że teraz rzucamy w płaski świat płaszczaków kulą. W którymś momencie dotyka ona płaszczyzny – świata robaków – i przelatuje przez nią. Zdumione robaki widzą najpierw punkt, który pojawia się znikąd i rozszerza się w linię, osiągającą maksymalną długość, kiedy równik kuli znajdzie się na płaszczyźnie robaków. To w rzeczywistości koło, ale robaki patrzą na nie z boku i widzą kreskę, jednak rozumieją jej "przestrzenne", płaskie, a nie tylko liniowe znaczenie. Potem linia zacznie się kurczyć, a wreszcie zniknie – równie tajemniczo, jak się pojawiła. Dla robaków będzie to niepojęty „cud”. A gdybyśmy zrobili to samo, opuszczając podkowiasty obiekt w kształcie U, robaki zobaczą najpierw rosnącą kreskę wydłużonego prostokąta, który podzieli się na dwa osobne, a i one z kolei po jakimś czasie trwania w bezruchu znów tajemniczo i tym razem gwałtownie znikną.

Wreszcie możemy sobie również łatwo wyobrazić, że z zamkniętej celi unosimy w górę czerwoną kropkę i stawiamy ją „na wolności”. Dla strażników będzie to tajemnicza teleportacja, niepojęte przejście przez ścianę – więzień najpierw zniknie – w nadprzestrzeni właśnie – opuszczając płaszczyznę wzdłuż trzeciego wymiaru, a potem z nicości tego wymiaru obcego płaszczakom pojawi się w innym miejscu, bez naruszania ścian celi.

Mistyczne doświadczenie robaków możemy teraz powtórzyć, używając naszego trójwymiarowego modelu, otwierając zawierającą go stronę lub programik do ściągnięcia i zainstalowania (znów – proszę tymczasem stronić od opcji "4D).

Jeśli włączyć niebieską opcję w lewej górnej części okna i kazać pokazać sobie „tysiące zamiast setek”, zobaczymy sześcian, jak zwykle. Jeśli włączymy opcję „pokaż wartości”, będziemy mogli zobaczyć, z jakich „warstw” składa się teraz nasza kostka – ułożonych jedna na drugiej wzdłuż pionowej niebieskiej osi. Najniższa warstwa zawiera liczby od 0 do 99, nad nią będzie warstwa z liczbami od 1000 do 1099, potem od 2000 do 2099 itd. Wybierzmy opcję „przekrój wzdłuż T = 0”, a zobaczymy świat płaszczaków. Będziemy patrzeć z góry, więc z perspektywy im niedostępnej – ale tak właśnie chcemy.

Suwak „przekrój wzdłuż Z =” będzie nam teraz zmieniał setki „w ramach pierwszego tysiąca” liczb. Manipulując nim, zobaczymy animację tego, co stałoby się w świecie płaszczaków, gdyby przezeń przeleciał trójwymiarowy sześcian liczb od 0 do 999 rozmieszczonych według reguł, które już dobrze znamy.

Duża przekątna z pierwszej setki w kolejnych setkach zacznie się przesuwać na lewo, zaś pojedynczy punkt z prawego górnego rogu zamieniony w kolejną skośną linię zacznie się przemieszczać do środka. W końcu utworzy przekątną, a dotychczasowa przekątna, która w pierwszej setce leżała dokładnie w tym samym miejscu, skurczy się teraz do kropki w narożniku. W prawym górnym rogu pojawi się zaś punkt, od którego zaczęłaby się nowa linia wędrująca w lewo, gdybyśmy mieli jakieś dalsze setki. Znamy już prawa podzielności przez 9 i wiemy skąd się bierze zjawisko.

Wyłączmy teraz na chwilę opcję przekroju wzdłuż T. Inaczej niż na wielu filmach SF, w których pokazuje się zazwyczaj uciekające w nieskończoność widoki nakładających się na siebie półprzezroczystych obiektów, my widzimy, że setki kolejnych tysięcy leżą w jednym miejscu – poszczególne kostki przestają być przezroczyste, właśnie dlatego, że jest ich w rzeczywistości wiele w jednym miejscu. W świecie, w którym to oglądamy – w naszym świecie, a nie tylko w świecie robaków – wymiar, który pozwala te miejsca rozróżnić, nie istnieje – w świecie bez tego wymiaru wiele różnych obiektów hiperprzestrzennych istnieje dla nas jednocześnie w tych samych miejscach.

Robaki płaszczaki to inteligentne stworzenia. Patrząc na liczby od 0 do 99 umieszczone w dobrze im znanym płaskim świecie, zadały już sobie pytanie „jak sobie wyobrazić tysiąc liczb”, co jest ich odpowiednikiem naszego pytania o dziesięć tysięcy. Wiedzą, że musiałyby dysponować trzecim wymiarem i że kolejne setki musiałyby leżeć gdzieś „ponad” ich światem. Dla nas to jest zwykłe „ponad” – dla nich jednak to samo „ponad” ma mistyczny posmak. Rozmaite życiowe doświadczenia upewniły je przecież, że ów wymiar jednak istnieje naprawdę. Kiedyś więc, w czasach u płaszczaków owianych legendą, najodważniejsi z płaskich śmiałków wybrali się na kraj świata. Przewidywano, że nigdy nie wrócą. Nikt nie wierzył, że „kres świata” da się zobaczyć – sądzono raczej, że świat jest nieskończony. Albo, że jakieś nieznane jeszcze prawo natury nie zezwoli na dotarcie do jego brzegu. Po długiej wędrówce podjętej w poszukiwaniu ostatecznych odpowiedzi śmiałkowie powrócili jednak do punktu wyjścia. Odtąd zaczęto podejrzewać, że świat jest zakrzywiony. A krzywizna leży w płaszczyźnie różnej od tej znanej płaszczakom. Inaczej nie da się wyjaśnić, dlaczego idąc wciąż przed siebie, jednak powrócili. Robaki okazały się nie tylko wystarczająco inteligentne, żeby to odkryć – to potrafiłby w zasadzie każdy na ich miejscu – ale jeszcze postanowiły odtąd wyjaśniać to robaczątkom w szkołach, a to już jest znak prawdziwego społecznego geniuszu. W rzeczywistości to jest również znak tego samego egzystencjalnego niepokoju, który i my dobrze znamy. Skoro świat okazał się skończony, pojawiło się dręczące pytanie, co jest poza nim. I nadzieja, że młodzi się z tym pytaniem zmierzą. Mamy okazję spojrzeć na taką lekcję. Oraz posłuchać opowiadania mądrych płaskich uczonych.

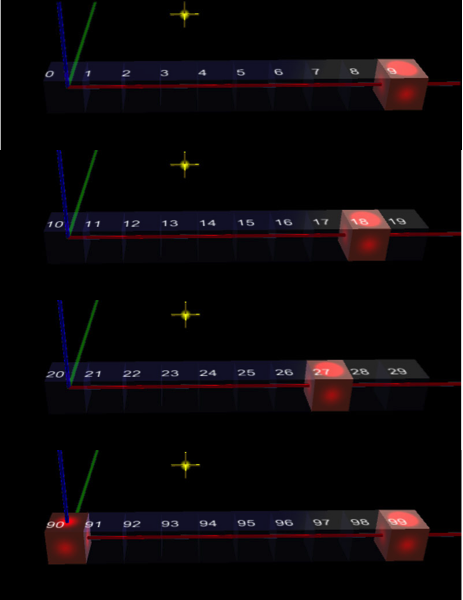
Wyobraźmy sobie – powiadają więc odtąd swoim płaskim maluchom mądre płaszczaki – małe robaki prostaki. Tak jak my możemy swobodnie poruszać się po naszym ogromnym, pięknym i przebogatym świecie, widząc na przykład nieskończoność jego osi, z których każda jest sama w sobie nieskończona, tak prostaki żyją tylko na jednej z tych osi i ich świat jest do niej ograniczony. Mogą poruszać się wyłącznie w przód i w tył i tylko w tym kierunku mogą patrzeć. Podobnie jak my, mają dwoje oczu, ale jedno z nich patrzy w przód, a drugie wyłącznie w tył. Nie są w stanie dostrzec przestrzeni i perspektywy zbiegającej się ku nieskończoności, ponieważ w ich świecie nie może istnieć żadna oś prostopadła, wzdłuż której mogłyby zmieniać się skale, albo chociaż ich obraz. Bliższe i dalsze obiekty mają w ich oczach ten sam punktowy rozmiar. Możliwe, że jakieś superczułe organy ich podłużnych ciał są w stanie rejestrować czas, po jakim światło dociera do nich z innych punktów na prostej, zależnie od odległości – i prostaki mogłyby w ten sposób postrzegać odległość. Każdy taki robak albo jest przy tym samotny, albo widzieć może co najwyżej dwa sąsiednie robaki po dwóch stronach siebie samego – o istnieniu pozostałych może tylko słyszeć od sąsiadów. Sąsiada nie da się ani ominąć, ani zza niego wyjrzeć na dalszy świat. I wyobraźcie sobie, drogie dzieci, co by się mogło stać, gdyby w ich prosty świat wtargnął nagle dwuwymiarowy obiekt – choćby kwadrat 100 liczb ułożonych dziesiątkami wzdłuż tej drugiej osi, której w świecie prostaków nie ma.

Pokaz o prostakach wykonany dla dzieci przez płaszczaki możemy odtworzyć na naszym modelu, każąc tym razem pokazać sobie tysiące zamiast dziesiątek, włączając równocześnie przekrój wzdłuż Z = 0 oraz wzdłuż T = 0. Manipulowanie suwakiem przekroju wzdłuż Y pokaże teraz przelot dwuwymiarowego kwadratu przez świat leżący na osi X. Prostak stojący w punkcie 0 zobaczy pojawiające się znikąd czerwone, podzielne przez 9 liczby: 18, 27 itd. – każda z nich coraz bliżej niego…

Spróbujemy się teraz postawić w roli płaszczaków studiujących niedostępny im trzeci wymiar i trudny do pojęcia model trójwymiarowego kwadratu, który dla nas jest oczywistą kostką. Potraktujemy to jako wprawkę przed znacznie trudniejszym dla nas zadaniem, w którym odtworzymy szczegóły budowy tesseraktu, bryły czterowymiarowej, opisującej pierwsze 10 tys. liczb w układzie dziesiętnym á la Montessori, poznając przy okazji niepojętą ideę zawartą w Ukrzyżowaniu Dalego.

Jeszcze raz uprzedzam, że będzie trudno. Obszerne wyjaśnienie poniżej jest dla tych, którzy patrzą na pokazaną obok, często stosowaną ilustrację i nie rozumieją z niej niczego – a chcieliby zrozumieć.

Dwie dygresje w tym miejscu. Pierwsza pochodzi jeszcze ze szkoły małych płaszczaków. Otóż wyjaśniwszy dzieciom ograniczoność świata oraz zmysłów robaków prostaków, płaszczaki opowiadają dzieciom o wstrząsającym odkryciu, którego prostaki zdołały dokonać w czasach dawnych i legendarnych. Otóż prosta linia, na której żyją te stworzenia, jest w rzeczywistości dużym okręgiem. Tak dużym, że krzywizny nie da się dostrzec, zresztą zakrzywieniu ulega w tym świecie wszystko, nawet światło biegnące od jednego robaka do drugiego, więc nawet przy stosunkowo małym promieniu krzywizny robaki i tak w żaden sposób nie mogłyby wykryć zakrzywienia, niezależnie od tego, że samo pojęcie krzywizny pozostaje poza zakresem ich pojmowania, skoro krzywizna wymaga więcej niż jednego wymiaru, żeby się dała zrozumieć. Dawno, dawno temu – opowiadają płaszczaki dzieciom – prostaki podjęły wysiłek godny herosów. Dwoje z nich pozostało na miejscu, by zapewnić przetrwanie gatunku, a wszystkie pozostałe udały się podróż. Wspólna wędrówka wszystkich była konieczna, skoro prostaki nie mogą się minąć (rozwój populacji dwupłciowych robaków, które nie mogą zamieniać się miejscami to osobne, ciekawe zagadnienie). Prostaki wędrowały długo w poszukiwaniu krańca prostej. Nie napotkawszy go zatoczyły niewyobrażalnie dla siebie koło i powróciły do miejsca, w którym przez długie lata czekała na nich pozostawiona samotna para z potomstwem, które w międzyczasie przyszło na świat. Prostaki odkryły zakrzywienie własnej przestrzeni. To było bardzo dawno temu, a jednak prostaki do dziś zastanawiają się, czy drugi wymiar przestrzeni istnieje rzeczywiście i świat ma się jak zakrzywiać, czy może jednak proste są w jakiś inny sposób cykliczne z natury. Albo może wszystko w tym jednowymiarowym świecie istnieje w nieskończenie wielu równomiernie rozmieszczonych i nierozróżnialnych kopiach. Łącznie ze świadomością. I jaźnią prostaków. Niby jak rozstrzygnąć i zdobyć dowód w tego rodzaju sprawie?

Dygresja druga ma bardziej techniczny charakter i jest niezbędnym wstępem o ewolucji idei kostki w przestrzeniach o rosnącej liczbie odkrytych wymiarów. Wyjaśnienia wymaga bowiem sama konstrukcyjna definicja kostki.

Zaczynamy od punktu. Przestrzeń nie ma tu jeszcze wymiarów. Oznaczmy punkt liczbą 0, przygotowując się do notacji w rodzaju kartezjańskiej w układzie współrzędnych. Odkrywszy świat „robaków prostaków”, a więc pierwszy wymiar, jesteśmy w stanie oznaczyć następny punkt. Ponieważ posługujemy się liczbami w systemie dziesiętnym, niech 10 będzie już zawsze odległością pewnych wyróżnionych w naszej konstrukcji par punktów, które staną się wierzchołkami naszych figur i brył w pęczniejącej wymiarami przestrzeni. Nasz drugi punkt będzie miał więc współrzędną 9 i będzie to – tymczasem – jego jedyna współrzędna, podobnie jak 0 jest jedyną współrzędną punktu „wyjściowego”.

Odcinek, para punktów {(0); (9)}, jest jedynym możliwym „kwadratem” w jednowymiarowym świecie prostaków. Jeśli jednak odkryjemy teraz drugi wymiar, co ulokuje nas w świecie płaszczaków, jesteśmy w stanie oznaczyć dwa dodatkowe punkty – każdy w odległości 10 od tych już ustalonych i każdy oddalony tylko wzdłuż tego nowego wymiaru. Prostopadle. Otrzymujemy kwadrat o wierzchołkach w czterech punktach, których współrzędne będą już teraz parami liczb:

{(0, 0); (0, 9); (9, 0); (9, 9)}.

Ocena ilości wierzchołków nie nastręcza trudności ani nam, ani robakom prostakom – dla prostaków wszakże policzenie ilości boków kwadratu może być już kłopotliwe. My dobrze wiemy, że kwadrat ma cztery boki i że nie każda para punktów tworzy bok. Przekątne nie są bokiem, leżą we wnętrzu kwadratu. Jak ma to jednak stwierdzić nasz biedny prostak, który tylko maksymalnym wysiłkiem zanurzonego w kompletnej abstrakcji umysłu rozważa własności figury, której ani zobaczyć, ani nawet plastycznie sobie wyobrazić nie może?

Otóż logicznie myślący prostak ma dwa narzędzia wspomagające jego wyobraźnię. Po pierwsze może się domyślić, że w dwóch wymiarach z każdego wierzchołka mogą wychodzić dokładnie dwa boki – inaczej niż w jego świecie, gdzie z wierzchołka może wychodzić tylko jeden bok. Przekątna byłaby trzecim bokiem, a to o jeden za dużo w dwóch wymiarach. Po drugie robak może też wiedzieć, że przekątna zdefiniowana jest taką parą punktów, w której obie współrzędne są równocześnie różne. Krawędzie nie powstają poprzez połączenie wierzchołków na "pucharowej" zasadzie "każdy z każdym". Popatrzmy, istotnie odcinki:

{(0, 0); (9, 0)},

{(0, 0); (0; 9)},

{(0, 9); (9, 9)},

{(9, 0); (9, 9)}

mają końce w punktach różniących się wartością tylko jednej współrzędnej i są w związku z tym bokami, podczas, gdy odcinki:

{(0,0); (9, 9)}

i {(9, 0); (0, 9)}

są przekątnymi. ponieważ obie współrzędne końców są równocześnie różne. Proszę sprawdzić to na komputerowym modelu, a rzecz stanie się jasna. To uniwersalne prawo konstrukcji kostki działa w każdej przestrzeni.

Zadanie płaszczaka nieco się komplikuje. Odkrywa trzeci wymiar, a my – niemal boskie istoty rodem z trójwymiarowego świata – doskonale znamy konsekwencje, które biedny płaszczak poznaje z mozołem. Cztery punkty kwadratu (który teraz stanie się podstawą nowej bryły) da się teraz połączyć w pary z ich odpowiednikami odległymi o 10 w stronę tego niewyobrażalnego dla płaszczaka trzeciego wymiaru. Płaszczak bez większego trudu domyśli się, że wierzchołków sześcianu będzie więc 8. Przepisując listę dla kwadratu i uzupełniając ją odpowiednio:

{(0, 0, 0); (9, 0, 0); (0, 9, 0); (9, 9, 0); (0, 0, 9); (9, 0, 9); (0, 9, 9); (9, 9, 9)}.

Ile będzie krawędzi? Jak je rozpoznać? A ile będzie ścian? Dla nas to są rzeczy oczywiste, dla płaszczaka – w najmniejszym stopniu! Zanim zaczniemy się z pobłażaniem uśmiechać, pomyślmy choćby o tym, czym mogą być ściany tesseraktu i jak je rozpoznać…

Włączmy koniecznie nasz komputerowy model, bo on właśnie zaczyna ujawniać swoje zalety. I przejdźmy do oferowanej nam, wygodniejszej notacji, w której współrzędne zamieniają się w liczby ułożone w kostki, jak w Montessori. Odcinek w świecie prostaka będzie miał końce w 0 i 9 – będą na nim leżeć wszystkie liczby w tego przedziału, więc np. 5 i 7. Ten odcinek zobaczymy, jeśli poza domyślnie włączoną opcją „przekrój wzdłuż T = 0” włączymy także „przekrój wzdłuż Z = 0” (dostaniemy w ten sposób kwadrat pierwszej setki) i następnie „przekrój wzdłuż Y = 0” (co pokaże pierwszą, właściwie zerową dziesiątkę liczb).

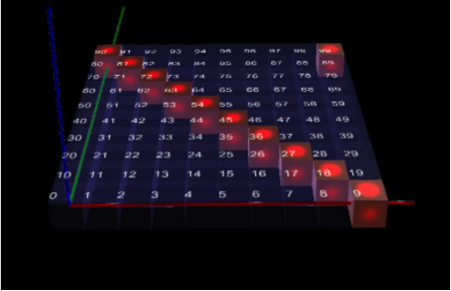
Kwadrat w świecie płaszczaka będzie miał wierzchołki w punktach: 0, 9, 90 i 99 (zobaczymy go odznaczając przekrój wzdłuż Y i pozostawiając ten wzdłuż Z – przekrój wzdłuż T musi być stale włączony, póki obserwujemy pierwszy tysiąc). Boki kwadratu będą teraz seriami liczb:

co jeden – 0, 1, 2, …, 9;

co dziesięć – 0, 10, 20,…, 90;

co jeden – 90, 91, 92,…, 99;

co dziesięć – 9, 19, 29,…, 99.

Spokojnie – myśli sobie płaszczak. Z punktu 0 w moim świecie wychodzą dwa boki. Jeden w stronę 9 i drugi w stronę 90. Gdyby istniała trzecia oś, oś setek… To nic, że jej nie zobaczę i w moim świecie nie ma jej gdzie umieścić... Bo niby gdzie? Pomiędzy X i Y? Tak czy siak, w odległości 10 (setek) od zera powinienem mieć liczbę 900. Trzecia krawędź będzie serią liczb co sto – 0, 100, 200, …, 900, rosnącą wzdłuż dodatkowego, trzeciego wymiaru. Eureka!

W trójwymiarowym świecie odkrycia płaszczaka wydają się oczywiste. Ale odtwarzając jego tok rozumowania korzystajmy na przemian z modelu trójwymiarowego oraz tego, w którym widzieć da się wyłącznie płaszczyznę – da się nań przełączyć przy pomocy przycisku z napisem „płaszczaki”, a potem powrócić stamtąd przyciskiem oznaczonym „3D”. Nie tylko zrozumiemy wtedy choć w części niemały ból płaskiej głowy wrzuconej w trójwymiarowy świat, ale i nabierzemy wprawy w poruszaniu się po omacku, co za chwilę przyda się nam w naszej własnej podróży w czwarty wymiar, którego przecież nie zobaczymy.

Trzeba przy tym pamiętać jeszcze o jednym. Płaszczak nie widzi płaszczyzny. Płaszczak na niej żyje. Widzi więc wyłącznie linie, być może zdolny do postrzegania w nich głębi, z pewnością rozumiejący perspektywę. Dwa wymiary rozumie doskonale, ale czy umie sobie przedstawić obraz płaszczyzny, jak choćby ten powyżej? Należałoby spytać płaszczaka, bo trudno wniknąć w cudzy umysł – wystarczająco kłopotliwe bywa przecież często, i będzie tym razem, zaglądanie we własny. Należy wątpić w tego rodzaju zdolności płaszczaka – nawet jeśli mamy do czynienia z płaszczakiem Picasso. Obraz powyżej wymaga umiejętności spojrzenia z trzeciego wymiaru. Jak zobaczymy w dalszej części, Picasso zmagał się z umiarkowanym tylko powodzeniem z obrazem trójwymiarowej struktury oglądanej z czwartego wymiaru, co odpowiada rozważanemu teraz problemowi wyobraźni płaszczaka. Trzeba o tym pamiętać, kiedy sami oglądamy wizerunek sześcianu. Widzimy wtedy coś jak kreskę, którą płaszczak ogląda na co dzień. Żeby obejrzeć sześcian naprawdę, tak jak sami spoglądamy na płaszczyznę – trzeba by zaś było zobaczyć coś jak obraz Picassa: sześcian z wszystkich jego stron równocześnie.

Płaszczak pracowicie myśli, eksperymentuje i wyciąga wnioski. I niestety my musimy robić to samo, czytając. W naszym komputerowym modelu płaszczaków możemy korzystać z opcji wyboru setek zamiast jednostek lub setek zamiast dziesiątek, żeby zobaczyć rozmaite płaskie przekroje przestrzennej bryły, którą płaszczak rozpaczliwie próbuje zbadać, ustalając, co będzie na wierzchołkach, krawędziach i ścianach. Przebywając w krainie płaszczaków mamy ten nieznany im i już tu opisany komfort spoglądania z góry. Możemy jednak w ten ich świat "zstąpić" tak manipulując ustawieniami widoku, by wylądować na płaszczyźnie i starać się patrzeć tylko z niej.

Płaszczak już dobrze rozumie, że teraz każdy punkt dobrze mu znanego kwadratu ma po prostu zero w liczbie setek, a gdzieś w nadprzestrzeni unosi się odpowiadający mu drugi punkt wierzchołkowy, który w liczbie setek ma dziewięć zamiast zera. I że jest tych zawieszonych w nadprzestrzeni punktów tyle, co wierzchołków kwadratu. Każdemu wierzchołkowi znanego w płaskim świecie kwadratu o współrzędnych (x, y) trzeba teraz nadać potrójne w trójwymiarowym świecie współrzędne (0, x, y) – a każdemu takiemu punktowi odpowiadać będzie nowy wierzchołek (9, x, y) zawieszony w nadprzestrzeni.

Jak już wiemy, dla 0 będzie to 900, a liczby 100, 200 itd. będą leżały na odpowiedniej krawędzi;

dla 9 wierzchołkiem "hiperprzestrzennym" będzie 909, a na krawędzi znajdą się 109, 209 itd.;

dla 90 – 990, z liczbami 190, 290 itd. po drodze

i wreszcie 999 dla 99, a do krawędzi należeć będą odpowiednio 199, 299 itd.

Co więcej, nowe punkty, zatem 900, 909, 999 i 990 (wymieniam w kolejności przeciwnej do kierunku zegara) trzeba jeszcze połączyć czterema dodatkowymi krawędziami, a więc:

od 900 do 909, z liczbami 901, 902 itd. po drodze;

od 909 do 999, z liczbami 919, 929 itd.,

od 999 do 990, z 998, 997 itd., tym razem malejąco, żeby zachować kierunek,

i od 990 wstecz co 10 aż do 900 ze znów malejąco wymienianymi tu liczbami 980, 970 itd.

Płaszczak zidentyfikował wszystkie wierzchołki, a nawet zauważył, co jest dość proste, że ilość wierzchołków kostki w \(n\) wymiarach musi być zawsze \(2^n\), skoro musi się podwajać z każdym nowym wymiarem, bo to wynika z konstrukcji hiperkostki. Liczba \(2^n\) bierze się również stąd, że w n-wymiarowej przestrzeni każdy punkt ma n współrzędnych, a każda z nich może przyjąć dla wierzchołków dwie skrajne wartości (to kombinatoryczne zagadnienie – można je przy okazji wyjaśnić dzieciom). Możliwości jest tu zatem właśnie \(2^n\). Ilość krawędzi policzyć jest już płaszczakowi trudniej. Ulega ona po pierwsze najpierw podwojeniu, skoro bryłę „wyjściową” (w przypadku płaszczaka na tropie sześcianu wyjściowy był kwadrat) najpierw kopiujemy, umieszczając ją na wysokości 9 w nowym wymiarze (tu w wymiarze liczby setek), gdzie krawędzie się powtórzą (w przypadku sześcianu będzie to drugi kwadrat zawieszony na wysokości 9 setek). Po drugie jednak do tej podwojonej liczby krawędzi należy dodać krawędzie łączące ze sobą w pary odpowiadające sobie wierzchołki kopii i oryginału, zatem tyle, ile jest wierzchołków bryły wyjściowej. Płaszczak wymyślił zatem, że dla trójwymiarowej kostki liczbą krawędzi będzie 12.

Co więcej, przenikliwy bądź tylko uparty, pracowity i zdyscyplinowany płaszczak zdołał również ustalić, że skoro sześcian ma 8 wierzchołków, tesserakt musi mieć ich oczywiście 16. Skoro sześcian ma 12 krawędzi, tesserakt musi ich mieć 2 x 12 = 24, do czego trzeba koniecznie doliczyć jeszcze 8 dla połączenia ze sobą wierzchołków dwóch sześcianów odległych od siebie o 10 na osi tysięcy, która będzie czwartą osią tego układu współrzędnych. Krawędzi tesseraktu będzie więc w sumie 32. Skoro krawędzi jest dwa razy więcej niż połączonych nimi wierzchołków, to z każdego wierzchołka będą wychodziły 32/16/2 = 4 krawędzie, podobnie jak dla sześcianu było ich 12/8/2 = 3.

Co jeszcze więcej, płaszczak wymyślił również regułę pozwalającą odróżnić parę wierzchołków wyznaczających krawędź, od tej, która byłaby przekątną. Wie nawet, że odcinek łączący wierzchołki, w których wszystkie trzy współrzędne są różne, więc np. {(0, 0, 0); (9, 9, 9)}, albo {(0, 0, 9); (9, 9, 0)}, byłby przekątną całej bryły, podczas gdy ten, w którym różnią się dwie współrzędne, jak to jest w przypadku {(9, 0, 0); (9, 9, 9)}, jest przekątną którejś ściany, choć sama ściana jest dla płaszczaka niepokojącym i trudnym zjawiskiem, o czym wkrótce przekonamy się na własnej skórze. Krawędziami są w każdym razie odcinki łączące punkty, w których dwie współrzędne są identyczne, a różnica dotyczy tylko jednej z nich, jak to się dzieje we wszystkich przypadkach boków dotąd opisanych. Wynika to ze sposobu konstrukcji kostki. Każda krawędź musi być równoległa do którejś z osi współrzędnych. Ta cecha krawędzi hiperkostki będzie uniwersalną zasadą dla każdej z wielowymiarowych przestrzeni. Proszę koniecznie obejrzeć to w modelu i skłonić się przed płaszczakiem, który „nie widział, a uwierzył”, choć on tylko ufał rozumowi…

Brawo dla płaszczaka, ale w trzech wymiarach pojawia się problem ścian! A w czterech tym bardziej! Fakt, że każde trzy punkty albo dwie przecinające się proste w przestrzeni tworzą płaszczyznę był dla płaszczaka dotąd niezauważalny. Płaszczak żył nie tyle na płaszczyźnie, co w jakimś sensie wewnątrz niej i nie miał dotąd pojęcia, że mogą istnieć inne płaszczyzny niż ta jego „ojczysta”. Właśnie zaczyna do niego docierać, że przez obszar, w którym aktualnie przebywa, w (nad)rzeczywistości przechodzi nieskończoność różnych płaszczyzn. Różnych co do trzeciego wymiaru, którego on nie jest w stanie dostrzec. Co więcej, uświadomił sobie właśnie, że w tym fizycznym miejscu płaszczyzny, które właśnie zajmuje i potrafi zidentyfikować przy użyciu tych dwóch wymiarów, które umie postrzegać i odróżniać i które są jego jedyną realnością, może równocześnie istnieć nieskończoność innych płaskich światów. Dałoby się je odróżnić trzecim wymiarem, ale płaszczak go nie widzi, więc nie umie powiedzieć, na ile one są rzeczywiste. Nie widzi więc tych światów „równoległych”, ale według miar jego własnego świata, one istnieją dokładnie w tym samym miejscu, w którym istnieje on sam! Powiedzmy, że to czas jest owym trzecim wymiarem – to jeszcze płaszczak umie sobie wyobrazić łatwo. Wtedy mógłby zaakceptować fakt, że jego przestrzeń nawiedzają duchy przeszłości, ale w każdym innym przypadku…

No dobra, płaszczak popadł w filozoficzne osłupienie na granicy solipsyzmu, ale ponieważ jest stworzeniem płaskim i bardzo rozsądnym, otrząsnął się z metafizycznych dreszczy i powrócił do konkretów. My pozostańmy przez chwilę w tym samym zadziwieniu i, wybiegając myślą nieco wprzód, zastanówmy się przez chwilę nad czekającym na rozwikłanie tesseraktem. No, czwartego wymiaru nie umiemy sobie wyobrazić i mamy wrażenie – być może niesłuszne, ale co z tego, skoro przemożne – że niemożliwość czwartego wymiaru ma jakiś obiektywnie bardziej zasadniczy charakter niż niemożliwość trzeciego wymiaru dla płaszczaka. No, bo gdzie on może być? I co oznaczać? Hiperprzestrzenna kostka liczb ma tu nieocenioną zaletę, ponieważ na pewno istnieje przy całej swojej niemożliwości – za chwilę zresztą ją obejrzymy i „obmacamy” kawałek po tysiącach kawałków. Jedną z rozsądnych propozycji byłoby nadać czwartemu wymiarowi np. sens inny niż przestrzenny. Tak mogłoby być, choć wcale nie musi – czasoprzestrzeń, jako się rzekło, jest jednym z przykładów, w którym czwartym wymiarem jest właśnie czas. Ale wzdłuż czwartej współrzędnej mogą się zmieniać różne inne rzeczy lub cechy obiektów. Np. temperatura. Jeśli wyobrazimy sobie, że w trzech przestrzennych wymiarach ułożono kostki dokładnie takie jak na tutejszych rysunkach, to kostki różniące się tylko czwartym wymiarem będą się różniły wyłącznie temperaturą. Przestrzennie natomiast zajmą to samo miejsce. Ta intuicja jest z całą pewnością lepsza niż próba wyobrażenia sobie jakiejś wykrzywionej osi, którą postanowiliśmy uważać za jakimś cudem prostopadłą do pozostałych w zwykłym, geometrycznym sensie. Wyobrażamy sobie wtedy, że kostki różniące się czwartą współrzędną są w różnych miejscach także w trójwymiarowej przestrzeni, a to jest nieprawda – są dokładnie w tych samych. Wszelkie ilustracje, pokazujące co innego, są z tego powodu fałszywe. Intuicja z temperaturą nie ma jednak zastosowania do kostki z liczb – bo wszystkie cyfry są jednakowe i każda grupa współrzędnych reprezentuje tę samą cechę liczby: jej wartość. No, powiedzmy…

Płaszczyzny płaszczak potrafi sobie wyobrazić i nawet w pewien ograniczony sposób zobaczyć. Wie też, że przekrój trójwymiarowej bryły będzie właśnie płaski – inaczej niż przekroje w jego świecie, które są wszystkie liniami. Uświadomił sobie, że brzeg takiej bryły to nie całkiem linia – to wycinek płaszczyzny. Zatem ściana. Ile ścian ma sześcian i co na nich jest? My to możemy zobaczyć, ale płaszczak musi wysilić rozum, bo oczy nie powiedzą mu niczego poza złudą rodem z jaskini.

Włączmy komputerowy model płaskiej przestrzeni płaszczaków (nadal unikając 4D) i koniecznie powtarzajmy na nim wszystkie tu opisane operacje, sprawdzajmy też samodzielnie rzeczy opisywane tu ogólniej. Najprostszym sposobem zobaczenia tego, co dzieje się na ścianach i krawędziach trójwymiarowej bryły będzie manipulacja suwakiem przekroju wzdłuż Z. Zobaczymy wtedy, co zobaczy płaszczak, kiedy przez jego płaski świat wzdłuż niewidocznej i dla płaszczaka niewyobrażalnej osi Z (osi setek) przeleci sześcian. W jego świecie pojawiać się będą kwadraty przekrojów. W pierwszym z nich zobaczy podstawę sześcianu i jej całą zawartość. Następne przekroje pokażą płaszczakowi m.in. zawartość pionowych krawędzi sześcianu – będą to liczby w wierzchołkach kolejnych kwadratów. Oraz zawartość ścian – a będą to tym razem liczby zawarte w czterech bokach przekrojowych kwadratów. Wreszcie na koniec płaszczak zobaczy „dach” – kwadrat na wysokości 9.

Proste, prawda? Cóż, kiedy powtórzymy to samo doświadczenie w świecie trójwymiarowym, manipulując tym razem podobnie skonstruowanym przekrojem kostki czterowymiarowej, nie będziemy rozumieli niczego – chyba, że jesteśmy jednym z tych bardzo nielicznych Czytelników, którym czterowymiarowych konstrukcji objaśniać nie trzeba. Nie zrozumiemy dlatego, że nie doceniliśmy trudności płaszczaka w sytuacji opisanej powyżej. To tylko my widzimy zmieniające się kwadraty. Płaszczak stoi w ich wnętrzu, albo poza nim – w każdym razie, jak już podkreślaliśmy, widzi kreski. Zwłaszcza liniowe zachowanie zaznaczanych na czerwono liczb podzielnych przez 9 jest dlań mylące. Rodzi sugestię, że kwadraty pojawiają się z głębi przestrzeni płaszczaka. W rzeczywistości pojawiają się „z góry”, czyli z kierunku, który dla płaszczaka nie istnieje. Mimo wrażenia zaglądania w głąb, płaszczak zdaje sobie przecież sprawę z tego, że kwadraty kolejnych setek nie są ułożone jeden za drugim, bo nie o to chodzi w dziesiętnych systemie. Patrząc w głąb któregokolwiek z kierunków n-przestrzeni da się zobaczyć zawsze tylko 10 rzędów liczb n-kostki. A nie 100. Pozostałe liczby są gdzieś poza tym kierunkiem. Są ułożone prostopadle do wszystkich kierunków, które płaszczak zna.

Płaszczak widzi i rozumie dwa wymiary. Jeśli więc włączymy opcję „setki zamiast jednostek” zobaczymy teraz kwadrat nieco innych liczb. Wzdłuż czerwonej osi liczb rosnąć nam będą teraz – zgodnie z nazwą opcji – setki: od 0 do 900. Oś zielona nie ulegnie zmianie – nadal pokazuje liczby w odstępach co 10: od 0 do 90 na krawędzi leżącej na osi, potem od 100 do 190 itd. Dla nas ten obraz sytuacji jest oczywisty, albo przynajmniej zrozumiały bez większego trudu. W płaskim mózgu robaczka nie jest jednak tak prosto. Najpierw robaczek zauważył, że punkt 0 należy do dwóch różnych kwadratów. I nie tylko punkt 0. Wykonajmy sztuczkę i zaznaczmy widoczne teraz liczby odpowiednim przyciskiem. Na zielono zabarwiły się nam wszystkie liczby kwadratu. A teraz wyłączmy opcję „setki zamiast jedności”. Widzimy kwadrat, którego jedna krawędź zaznaczona jest na zielono. Odpowiedni napis informuje nas, że zaznaczona pozostaje nadal setka liczb, choć teraz widzimy ich tylko 10. To jest wspólna krawędź dwóch ścian. Będziemy z tego spostrzeżenia mogli skorzystać konstruując siatkę sześcianu, obserwując wspólne krawędzie i je oznaczając, by identyfikować, które kwadraty się ze sobą łączą i którymi bokami.

Włączmy na powrót opcję „setki zamiast jedności”. Używając suwaka „przekrój wzdłuż X” zmieniamy wartość pokazywanych jednostek, mimo, że wzdłuż tej osi rosną nam teraz setki – nieco to dziwne, ale wygodne. Uzmysławia to płaszczakowi kształt studiowanej bryły. W położeniu X = 0 ogląda mianowicie zaznaczoną teraz na zielono ścianę wystającą wzdłuż niepojętego dlań trzeciego wymiaru z osi Y w kierunku liczb od 900 co 10 do 990. Ta ściana teraz po prostu leży w jego świecie odwrócona na skutek zamiany współrzędnych. Zmieniając wartość X widzimy już nie ścianę, a kolejne przekroje sześcianu płaszczyznami prostopadłymi do osi jednostek – aż do momentu, kiedy X osiągnie wartość 9 i zobaczymy ścianę przeciwległą. Zaznaczmy liczby na tej ścianie. Ilość zaznaczonych liczb wynosi teraz 200. Wyłączmy opcję „setki zamiast jedności”. Widzimy zaznaczone na zielono już dwie krawędzie podstawy.

Obraz zaznaczeń nie zmieni się, jeśli włączymy teraz z kolei „setki zamiast dziesiątek” – zmienią się jednak wartości wyświetlanych liczb. Widzimy mianowicie inną ścianę pionową. Zaznaczmy liczby na tej ścianie. Liczba zaznaczeń wzrosła tym razem do 280 – to jedna z konsekwencji przyjętego modelu – krawędzie mają swoją grubość i powierzchnie ścian nie dodają się jak u Euklidesa, ponieważ część kostek jednostkowych się pokrywa. Przesuńmy się w górę do Y = 9 po drodze patrząc na przekroje. Zaznaczmy przeciwległą ścianę (liczba zaznaczeń: 360).

Włączmy opcję „setek zamiast dziesiątek” i wróćmy do kwadratu podstawy, na której nasz płaszczak czuje się pewnie. Widzimy zaznaczone wszystkie cztery boki. Manipulując suwakiem przekroju wzdłuż Z potwierdzamy domysł, że krawędzie wszystkich przekrojów są już zaznaczone – należą do oglądanych przed chwilą ścian. Ustawmy Z = 0, zaznaczmy ścianę podstawy i Z = 9, zaznaczając też „dach”. Zaznaczyliśmy w sumie 488 liczb leżących na brzegach sześcianu. W jego wnętrzu pozostało 512 liczb niezaznaczonych. Od tej pory każdy możliwy kwadratowy przekrój naszej bryły będzie miał wszystkie boki zaznaczone (prostokątny zresztą też, trójkątny i każdy, gdyby nasz model zapewniał możliwość krojenia na różne sposoby), ponieważ wszystkie ściany zostały zaznaczone. Ścian jest sześć – dwa razy tyle, ile wymiarów przestrzeni, co rozumiemy, wiedząc jak zaznaczaliśmy po dwie skrajne wartości trzech możliwych w trzech wymiarach przekrojów prostopadłych.

Domyślamy się więc, że ścian kostki czterowymiarowej powinno być osiem. I jest, ale tkwi w tym spostrzeżeniu pewien niepokojący szczegół. Ile jest ścian w dwuwymiarowym świecie płaszczaka? \(2 \cdot 2 = 4…\) Ale to są boki kwadratu... Niezupełnie wyglądają jak ściany. A w świecie prostaka? Cóż \(2 \cdot 1 = 2\). To dwa końce odcinka. Jak, na Boga, będzie w takim razie wyglądało 8 ścian tesseraktu?

Domyślamy się, że są trójwymiarowymi sześcianami, ale wcale nas to nie uspokaja – jak sobie coś takiego wyobrazić? Możemy te „ściany” szybko przejrzeć w komputerowym modelu. W domyślnym widoku 3D włączony jest przekrój wzdłuż niewidocznej tu osi T ustawiony na wartość 0. Zmieniając wartość suwaka widzimy kolejne sześcienne przekroje. Rozumiemy, że obserwujemy kolejne tysiące liczb, widzimy po prostu kolejne trójwymiarowe kostki, ale konstrukcji czterowymiarowej nadal przecież nie umiemy pojąć. Jest z nami jak z płaszczakiem, który oglądając sześcian, oglądał w rzeczywistości „multiświat” nie tyle przecież złożony z sześciu płaskich światów, co nimi tylko ograniczony. Podobnie jak to robił płaszczak, możemy teraz pozamieniać współrzędne i oglądać kolejne „ściany” (nazwijmy je teraz komórkami) i kolejne „przekroje”. Zaznaczmy szybko liczby ośmiu trójwymiarowych ścian, jak poprzednio płaszczak zaznaczył ściany sześcianu. W domyślnym przekroju wg T ustawmy się na obie skrajne pozycje suwaka, zaznaczmy widoczne liczby dla każdej z nich, a potem przełączajmy osie tysięcy kolejno na X, Y, Z i dla każdej z nich powtarzajmy operację. Nie przyglądajmy się na razie przekrojom – prawdopodobnie nie na wiele nam się to zda. Odkryjemy więc tylko, że we wnętrzu zostanie tam 4096 niezaznaczonych liczb i może nawet zauważymy, że to 8 razy tyle, co w przypadku sześcianu. Przy tej okazji – w przypadku kwadratu zostałoby ich 64; w przypadku odcinka – 8. To kolejne potęgi ósemki, ale… – czy to nam cokolwiek wyjaśnia? Jak można w ogóle mówić o „wnętrzu” czegoś, co ma przestrzenny brzeg?

Wyjaśnijmy przy okazji nieco dziwny sens tego, że przekrój bryły może nie być płaski. No, to zależy od punktu widzenia. Jeśli przekrój rozumiemy jako część wspólną płaszczyzny zrozumiałej dla płaszczaka i dla nas z jakąkolwiek inną bryłą, to w efekcie możemy dostać wyłącznie wycinek płaszczyzny i to niezależnie od tego, jak wielowymiarową bryłę przekroimy. W naszym komputerowym modelu możemy dostać również płaskie przekroje i wielokrotnie już je widzieliśmy. Problem po prostu polega na tym, że aby zidentyfikować płaszczyznę w czterech wymiarach, potrzebujemy – jeśli to ma być płaszczyzna ortogonalna, tj. równoległa do którejś pary osi współrzędnych – ustalić dwie z czterech współrzędnych, podczas, gdy w trójprzestrzeni wystarczy ustalenie jednej. Przekrój rozumiany jako ustalenie jednej współrzędnej, oznacza eliminację jednego z wymiarów przestrzeni. Co przy okazji w inny sposób tłumaczy, dlaczego patrząc z czwartego wymiaru na trójwymiarową bryłę, widzimy ją z każdej strony równocześnie – jak Picasso widział Dorę Maar.

Już płaszczak wymyślił, że tesserakt musi mieć 32 krawędzie i one są najzupełniej zwykłymi odcinkami. Czy poza 8 komórkami ta bryła ma jakiekolwiek normalne, płaskie ściany? Jeśli tak, to ile ich jest, jak wyglądają? Nasz ból głowy okazuje się nie tyle odpowiednikiem bólu głowy płaszczaka, ale właśnie jego kolejną potęgą, jeśli nam wolno tak rzec. Jest co najmniej ośmiokrotny.

Radą jest postąpić, jak postąpił rozsądny płaszczak. Należy odstawić wyobraźnię na bok, odrzucić od siebie mistyczne niepokoje i spróbować zimnych kalkulacji. Zadanie jest przed nami skomplikowane, ale pojęciowo nietrudne, jeśli właśnie wyłączymy wyobraźnię, bo tak się tym razem dziwnie składa, że to właśnie ona więzi nas w jaskini Platona…

Należy najpierw zdefiniować sobie wierzchołki bryły. To łatwe. Następnie trzeba spróbować zrozumieć, jakiego rodzaju obiekty (komórki, ściany, krawędzie) łączą się w wierzchołkach, co dokładnie (jakie liczby) zawierają i jak się łączą. Dopiero potem można pozwolić, by włączyła się wyobraźnia – ostrożnie i bardzo powoli, a ona wtedy zrobi to, co do wyobraźni należy. I co zrobić się da. Odwagi!

Wróćmy do liczby kostek we wnętrzu, a może trochę nas to uspokoi. Zazwyczaj w tym miejscu jesteśmy tak skołowani, że nie umiemy zauważyć banalnej logiki potęg ósemki. Rzeczywistość jest prosta. \(512 = 8 \cdot 8 \cdot 8\): to jest po prostu objętość sześcianu o krawędzi 10, „obranego” z powierzchni o „grubości” 1. Wynika z tego, że wnętrze tesseraktu \(8 \cdot 8 \cdot 8 \cdot 8\) musi być najzupełniej normalnym wnętrzem, choć mierzy się je (jego objętość) czwartą, a nie trzecią potęgą. No, akurat tego się przecież spodziewaliśmy.

Porzucając oglądanie modelu przyprawiającego o zawrót głowy za każdą próbą wyobrażenia go sobie w całości zamiast widzianych w nim przekrojów, wymieńmy najpierw wierzchołki tesseraktu. Modelu używajmy teraz wyłącznie do oglądania potwierdzenia hipotez – tak, jak to robił płaszczak w przypadku sześcianu. Sześcian, jak już bardzo dobrze wiemy, ma osiem wierzchołków:

0000;

0009;

0099;

0090

w podstawie oraz

0900;

0909;

0999;

0990

wierzchołków zawieszonych w górze.

Jak widzimy, na czerwono wstawiłem tu zera, co oznacza dodanie dodatkowej współrzędnej, wzdłuż której rosnąć nam będzie w tej (cztero)przestrzeni liczba tysięcy. Znów od 0 do 9. Banał przecież. Przypomnijmy sobie historię i znaczenie cyferek zabarwionych tu na zielono. W świecie płaszczaka cyferki były dwie. Pierwszym krokiem było ustalić, że kwadrat wyznaczony czterema pierwszymi wierzchołkami ma zerową trzecią współrzędną i jest wobec tego podstawą nowej, nieznanej płaszczakowi bryły w niepojętych dlań trzech wymiarach. Zielone cyferki, liczba setek, wyznaczają wysokość, trzeci wymiar sześcianu.

Lista powyżej zawiera zatem połowę wierzchołków tesseraktu – opisujących jego podstawę. Lista wszystkich wierzchołków zaś powstaje poprzez dwukrotne wydłużenie powyższej i zastąpienie zer dziewiątkami, a wygląda następująco (zachowajmy kolory):

0000;

0009;

0099;

0090;

0900;

0909;

0999;

0990;

9000;

9009;

9099;

9090;

9900;

9909;

9999;

9990.

Osiem punktów z czerwonymi zerami i osiem z dziewiątkami. Jak pamiętamy wierzchołek kwadratu o pisanych tym razem bez przecinków współrzędnych (00) łączył dwa boki, których drugie końce miały współrzędne odpowiednio (09) i (90). Odcinek {(00), (99)} nie jest bokiem, tylko przekątną, ponieważ nie jest równoległy do żadnej z dwóch osi współrzędnych, czego „objawem” jest równoczesna nierówność obu współrzędnych.

Ten sam punkt oznaczony tym razem jako (000) łączy trzy krawędzie sześcianu, na których drugich końcach znajdują się oczywiście (009), (090) i (900). Znów – tylko jedna współrzędna może być różna, żeby odcinek na pewno był krawędzią. Dwie z tych trzech krawędzi są równocześnie krawędziami kwadratu. Tylko trzecia z nich wystaje „w nadprzestrzeń” równolegle do trzeciego wymiaru – w stronę punktu (900).

Teraz z kolei punkt (0000) wyznaczy nam cztery krawędzie o końcach w punktach (0009), (0090), (0900) i (9000). I znów jedynie czwarta krawędź leży w nadprzestrzeni zmierzając wzdłuż czwartego wymiaru w stronę punktu (9000). Proste, prawda?

Co więcej, niemal cała robota z tesseraktem jest już w zasadzie wykonana. Reszta jest prostą, choć trudną do wyobrażenia konsekwencją tej konstrukcji. Wyobraźnię więc konsekwentnie „trzymamy wyłączoną”. Moglibyśmy teraz wziąć kartkę papieru, spróbować na niej rozmieścić szesnaście wierzchołków oznaczonych współrzędnymi, rozrzucając je po kartce z umiarkowanym tylko sensem, a następnie łączyć je ze sobą kreskami krawędzi według tego wzoru: z każdego wierzchołka mają wychodzić cztery krawędzie.

Powstrzymajmy się jednak i spróbujmy najpierw „domknąć” ściany, które się w tym wierzchołku spotykają. Ile ich jest? W sześcianie były trzy. Weźmy więc wierzchołek (0009) i wskażmy jego krawędzie, wyliczając drugie końce. Zróbmy to koniecznie samodzielnie na kartce papieru. Jeden już oczywiście mamy: (0000). Wiemy jeszcze z ustaleń płaszczaka, że krawędzie sześcianu muszą być równocześnie krawędziami tesseraktu, dla którego ów sześcian jest „podstawą”. To łatwo widać – pierwsza współrzędna (tysięcy) jest na każdym wierzchołku sześcianu równa 0, pozostałe różnią się w tworzących krawędzie parach wyłącznie jedną ze współrzędnych, więc w tesserakcie ten warunek oczywiście będzie również musiał być spełniony. Wiemy także, że również tym razem zaledwie jedna krawędź będzie nowa – ta która „wystaje” w czwarty wymiar. Bez większych kłopotów wskażemy więc drugi koniec tej krawędzi „wystający w nadprzestrzeń” z punktu (0009) – będzie to koniecznie (9009). Jak pamiętamy, w czwarty wymiar od punktu (0000) odchodziła krawędź zakończona w punkcie (9000), a para punktów {(9009), (9000)} różni się tylko jedną współrzędną, więc tworzy krawędź. Krawędź zamyka cykl, znaleźliśmy więc najwyraźniej kwadratową ścianę tesseraktu, zaczepioną na płaszczyźnie podstawy do krawędzi leżącej na osi X pomiędzy liczbami 0 i 9 (punkty (0000) i (0009)) i „pionową” wzdłuż osi T do punktów (9000) i (9009). Znamy inne ściany wychodzące z tej samej krawędzi. Jedna jest taka sama, jak stara ściana podstawy sześcianu: {(0000), (0009), (0099), (0090)}. Jest i trzecia: {(0000), (0009), (0909), (0900)} – też już widzieliśmy ją w sześcianie.

Trzy kwadratowe ściany z jednej krawędzi – w sześcianie były dwie. Wierzchołek sześcianu wieńczył trzy ściany rozpięte pomiędzy trzema krawędziami. Domyślamy się, że w tesserakcie pomiędzy czwórką krawędzi wychodzących z każdego wierzchołka, zmieści się... – no, ile się zmieści? 4 krawędzie po trzy ściany z każdej. 12? Ee… – chyba dwie krawędzie z tego samego wierzchołka tworzą wspólną ścianę, więc wyjdzie mniej. Ile wyjdzie? To teoria grafów, w której jestem kiepski, muszę narysować, inaczej nie zobaczę, choć – jak mi słusznie zwraca uwagę Ksawery Stojda – to jest proste zagadnienie kombinatoryczne widoczne na trójkącie Pascala. Do każdej ze ścian należą jakieś dwie krawędzie spośród czterech spotykających się wierzchołków. Różnych par z 4 elementów do wyboru da się zaś dobrać 6. Wyprzedzając więc rysunek – płaskich ścian będzie 6, co ktoś mądrzejszy ode mnie umie bez trudu wymyślić bez rysowania… A kombinatoryczne zagadnienie – jedno z wielu tu występujących – można znów spróbować wyjaśnić dzieciom.

Możemy teraz spróbować zacząć rysować, żeby się w tym wszystkim nie pogubić, pamiętając wszakże, że mamy bardzo marne szanse na wierny rysunek. W końcu papierowe szkice trójwymiarowego sześcianu są już mocno zniekształconym obrazem rzeczywistego kształtu – choć do takiego zniekształcenia przywykliśmy po prostu patrząc na świat, a widząc w rzeczywistości (kiedy zamkniemy jedno oko i pozbędziemy się stereoskopii) rzut, rodzaj cienia właśnie, na płaszczyznę. Uniknąć zamieszania i wynikającego zeń niezrozumienia da się wyłącznie rysując samemu, powtarzając opisane tu rozumowania prowadzące do stawiania poszczególnych kropek i kresek. Proszę spróbować koniecznie samodzielnie – bez tego nie da rady.

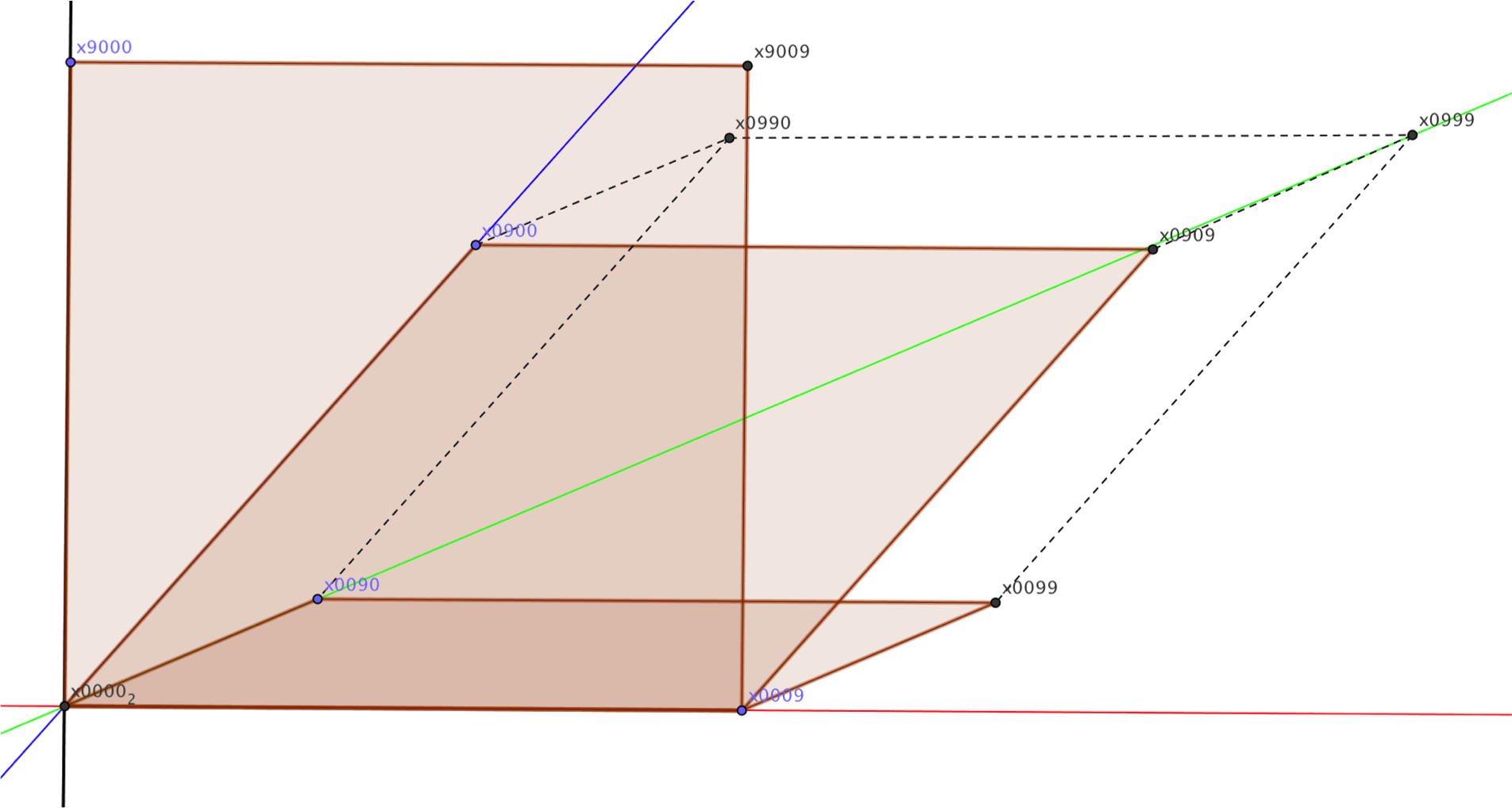
Szkic powyżej zawiera ustalenia poczynione dotychczas. Chociaż takich rysunków i nawet animacji używa się dla wyobrażenia brył czterowymiarowych, to niemal nigdy nie umieszcza się na nich osi współrzędnych, jak tu zaznaczone. Czerwona oś X jest osią jednostek, zielona oś Y jest osią dziesiątek. Niebieska oś setek Z jest tu nachylona w stronę płaszczyzny XY, równomiernie w stosunku do obu tych osi i trzeba sobie zdać sprawę z tego, że nie istnieje taki kąt, z którego patrząc zobaczylibyśmy taki obraz. Czarna oś pionowa jest osią nadprzestrzeni – to T, oś tysięcy. Przerywane linie to krawędzie sześcianu zbadane już przez płaszczaka – są one również krawędziami tesseraktu. Półprzezroczysty kolor oznacza odnalezione dotąd płaskie ściany tesseraktu przechodzące przez oś X, czyli krawędź zawierającą w naszym modelu liczby od 0 do 9.

Par wierzchołków zaznaczonych tu ścian, które są poza czerwoną osią, nie da się ze sobą połączyć krawędziami. Podobnie jak nie tworzy krawędzi (ani sześcianu, ani tesseraktu) np. para liczb (0099) i (0909) – a są to wierzchołki sześcianu tysiąca liczb – tak nie tworzy jej para (0909) i (9009). Różnią się tu dwie współrzędne, a nie jedna – co oznacza, jak zauważył jeszcze płaszczak, że odcinki o takich końcach byłyby przekątnymi ścian. Jeśli spojrzymy na wykoślawiony na tym szkicu sześcian, dostrzeżemy to z łatwością.

Zatem podobnie, jak w znanym nam dobrze, zwykłym sześcianie pomiędzy krawędzią {(0090), (0099)}, a {(0900), (0909)} (przy czym zera na początku oznaczają liczbę tysięcy i lokują nas w czterowymiarowej przestrzeni) musi istnieć dodatkowa krawędź {(0990), (0999)} , tak pomiędzy „nadprzestrzennie pionową” ścianą wzdłuż osi T, a zwyczajnie pionową ścianą wzdłuż osi Z (obie są wzajemnie prostopadłe, cokolwiek to znaczy) musi istnieć dodatkowa krawędź. Wyznaczą ją wierzchołki (0900) i (0909) przesunięte do skrajnej pozycji wzdłuż osi T, zatem (9900) i (9909) – jak zauważymy, dadzą się połączyć krawędziami z widocznymi najwyżej na szkicu punktami (9000) i (9009). Zbudowaliśmy sporo płaskich ścian i choć tego jeszcze nie spróbowaliśmy, widzimy, że potrafimy bez większego trudu odgadnąć każdą liczbę, która na nich leży, podobnie jak umiemy nazwać każdą z liczb każdej krawędzi, niezależnie od tego, jak skomplikowane i żmudne jest to zajęcie. No, problem w tym, że wzdłuż osi T należy jeszcze przesunąć mnóstwo innych punktów, w tym np. te położone z tyłu podstawy wyjściowego sześcianu: (0090) i (0099), dodając punkty o współrzędnych (9090) i (9099). Kolejny szkic dodaje dwie pary wierzchołków, dwie nowe krawędzie i dwie nowe ściany – zaznaczone tu na zielono.

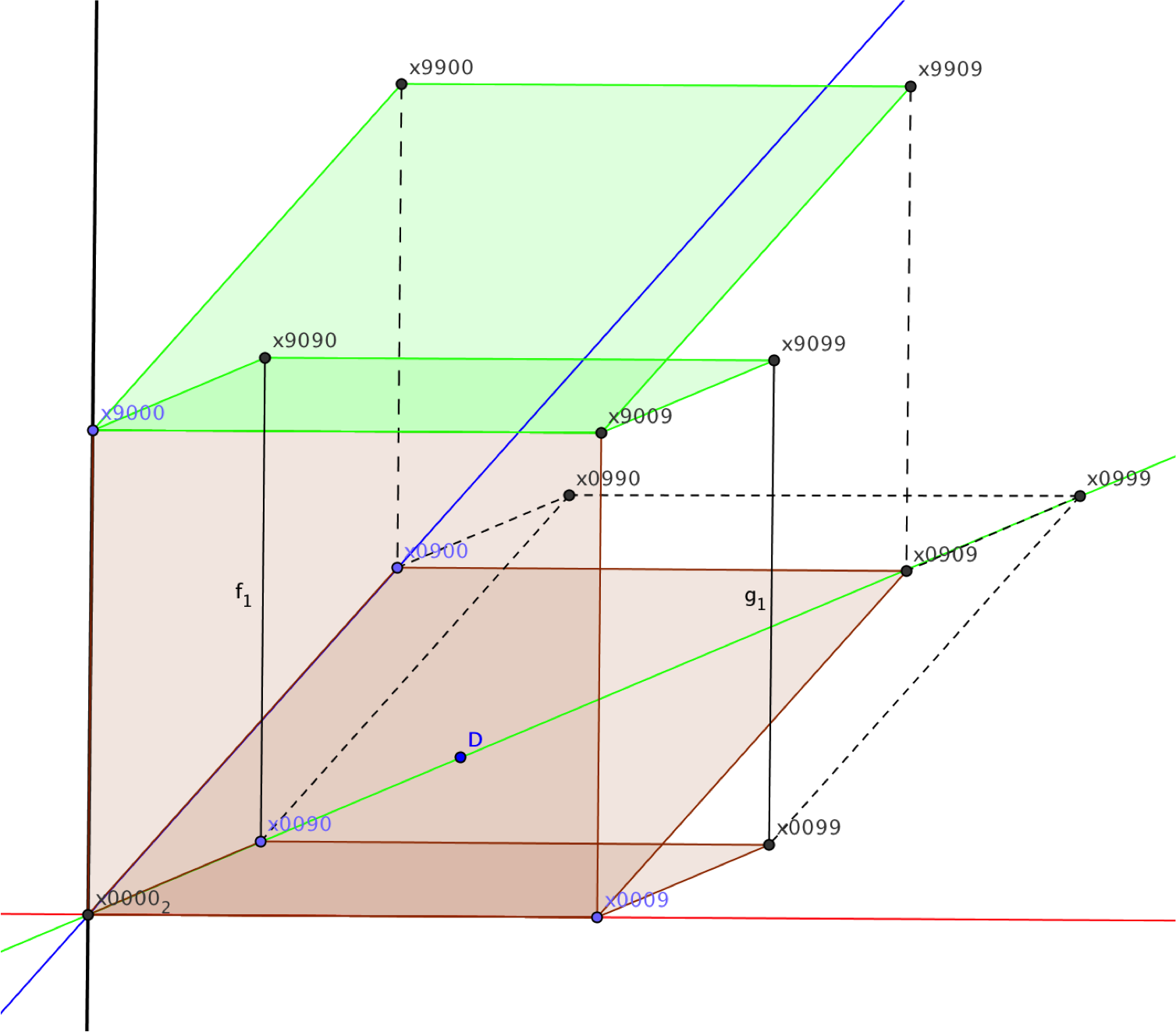
Obawiam się, że obraz traci na czytelności i powoduje kolejny zawrót głowy. Widzimy powstawanie plątaniny sześcianów, które zdają się przenikać w jakiś dziwny sposób.

No, zanim całkiem zwariujemy, skoro do tego stopnia brak nam talentu, porzućmy na chwilę samodzielne rysowanie i sięgnijmy po „gotowca” (w stosunku do powyższego szkicu ten poniższy jest nieco obrócony wokół, powiedzmy, osi Z – w rzeczywistości czteroprzestrzeni obroty są nieco bardziej zawiłym zjawiskiem):

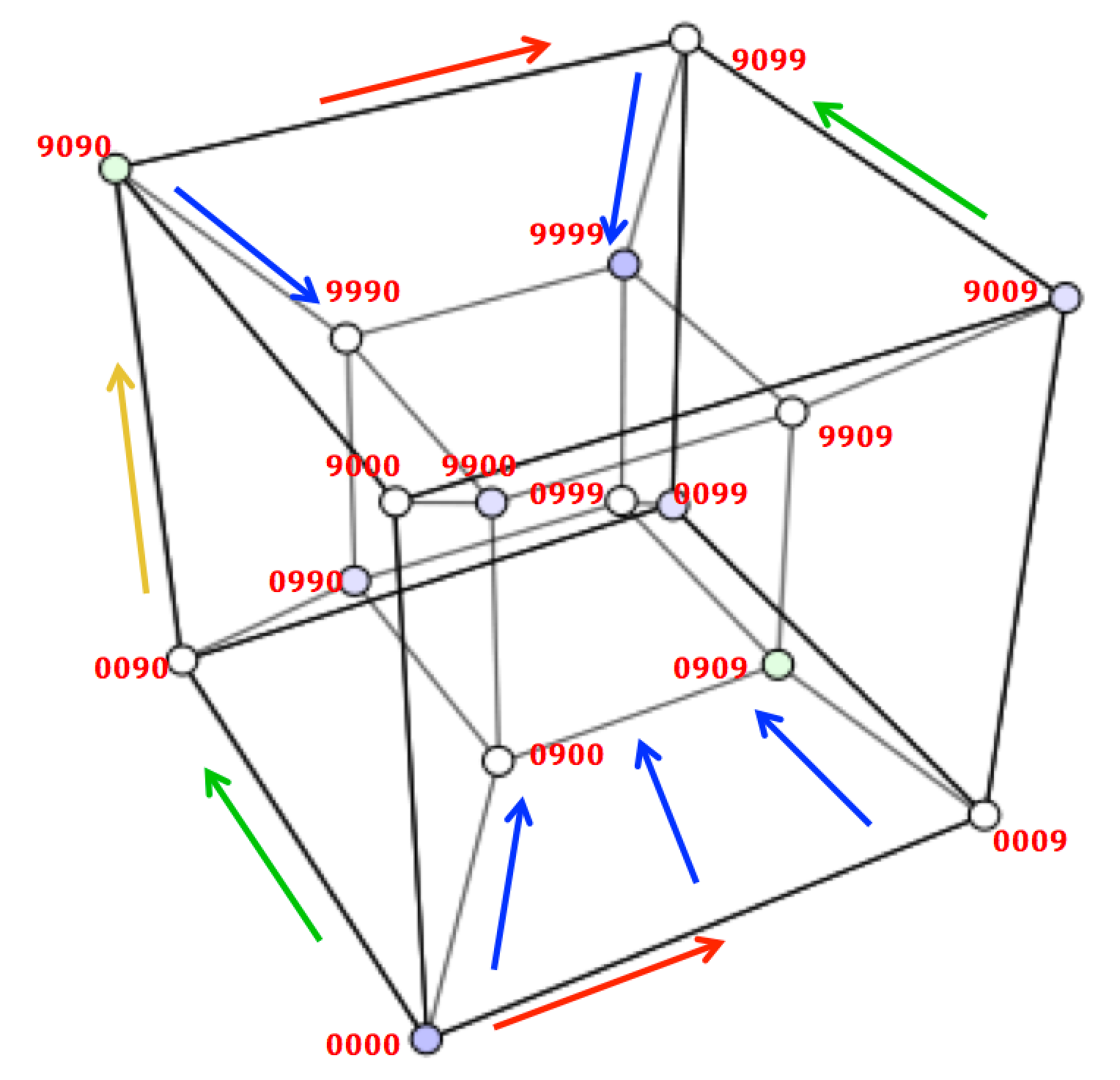
Jeśli przypatrzymy się temu rysunkowi uważnie, zobaczymy sześcian w sześcianie i to jest najbardziej popularna „wizja” tesseraktu. Do perspektywy tu ujętej nie ma co się przywiązywać, choć ten szkic jest jak najbardziej poprawnym rzutem perspektywicznym – jak widać liczby tu rosną w różnych kierunkach i nie ma tu żadnej konsekwencji. No, dzieje się tak dlatego, że kierunki są cztery, co musi powodować chaos i zafałszowanie perspektywy. „Zobaczyć” hiperbryłę znaczy zrozumieć zafałszowanie jej obrazu. W gruncie rzeczy moglibyśmy umieścić na płaszczyźnie niemal dowolnie 16 punktów – byleby tylko oznaczyć je i połączyć zgodnie z regułami ustalonymi jeszcze przez przenikliwego płaszczaka. Ten rysunek jest jednak precyzyjny – choć nie bardzo jest to widoczne – bo zachowuje równoległość części krawędzi. Myląca jest tu oś w naszym modelu oznaczana na niebiesko jako Z, wzdłuż której rośnie ilość setek. Równoległość jest tu zniekształcona perspektywą (jest to przy tym perspektywa czteroprzestrzeni, a nie płaskiego wyobrażenia, które widzimy) , co powoduje „wrażenie” zmiany kierunków. Albo wrażenie perspektywy, które jednak jest mylące, bo chodzi o specyficzną (czterowymiarową) perspektywę i właśnie ją trzeba tu zrozumieć. Z każdego wierzchołka wychodzą cztery krawędzie. Zakładając, że wszystkie kąty są tu proste i każda odpowiednio połączona ósemka punktów wyznacza sześcian – ile sześcianów widzimy? Na każdą ścianę małego sześcianu w środku przypada po jednym sześcianie spłaszczonym i wykrzywionym. Ósmy sześcian zamyka całość. No, oczywiście wszystkie te sześciany muszą być równe, żaden nie może leżeć we wnętrzu drugiego. Co wobec tego widzimy? Cóż, diagram, który mógłby być fragmentem osobnych zajęć o grafach. Linie diagramu odpowiadają jednak czemuś rzeczywistemu. Czemu?

Przyjrzyjmy się niektórym z widocznych tu sześcianów, zobaczmy co zawierają na krawędziach, ścianach i we wnętrzach, sprawdzając to w komputerowym modelu. Widzimy 8 sześcianów, 24 płaskie ściany, 32 krawędzie, 16 wierzchołków. Co z tego jest np. wnętrzem, a co brzegiem tesseraktu?

Jeden z sześcianów, które widzimy. to dobrze nam znany sześcian „wyjściowy” (choć teraz wykoślawiony) opisany wierzchołkami:

{(0000), (0009), (0099), (0090), (0900), (0909), (0999), (0990)}.

Szećian pierwszego tysiąca liczb – "podstawa" tesseraktu, jak kwadratowa podstawa sześćianu. Poza nim weźmy jeszcze:

{(0000), (0009), (0099), (0090), (9000), (9009), (9099), (9090)}.

Oba mają wspólną płaską podstawę zawierającą pierwszą setkę liczb. Różnią się „kierunkiem jej przesunięcia”. W trójwymiarowej przestrzeni nie mieliśmy pod tym względem wyboru. Mogliśmy to zrobić wyłącznie wzdłuż osi Z. Teraz dysponujemy osiami Z i T, które są obie prostopadłe do płaszczyzny XY i równocześnie (jakkolwiek niemożliwe jest takie dziwactwo) prostopadłe względem siebie. Jaki jest dokładnie rezultat takiej ekstrawagancji? Sprawdźmy. Zawartość sześcianów, ścian i krawędzi.

Pierwszy z sześcianów zobaczymy w domyślnym widoku po uruchomieniu programu. Żeby zobaczyć drugi, trzeba włączyć opcję „tysiące zamiast setek”. Wtedy podstawą oglądanego sześcianu pozostanie kwadrat od 0 do 99, natomiast „dachem” będzie kwadrat utworzony przez setkę liczb od 9000 do 9099 – tak, jak chcieliśmy. Na ile nakładają się te sześciany? Sprawdźmy, wybierając opcję „zaznacz” w tym drugim widoku, a potem wróćmy do widoku domyślnego, odznaczając wszystkie opcje, które trzeba w tym celu odznaczyć. W sześcianie pierwszego tysiąca liczb zobaczymy zaznaczoną na zielono podstawę. To nasz model, a nie szkic powyżej, pokazuje nam prawdę. Na szkicu widzimy maleńki sześcian „wyjściowy” z pierwszym tysiącem liczb, spłaszczony, „na dnie” i oczywiście wewnątrz tego drugiego tu rozważanego. W rzeczywistości – zwracam uwagę na dziwnie w tej sytuacji brzmiące słowo „rzeczywistość” – oba sześciany stykają się jedną ze ścian. Jak to możliwe?

To bardzo proste. Wszystkie liczby leżące w pierwszym sześcianie (tym od 0 do 999) powyżej podstawy, czyli pierwszej setki, „odstają” od podstawy w kierunku osi Z. W drugim sześcianie podstawa jest ta sama, ale kolejne warstwy – sprawdźmy w eksploratorze – różnią się od siebie o 1000, a więc „odstają” oczywiście wzdłuż osi T. Poza podstawą, gdzie w obu sześcianach wszystkie współrzędne są równe, pozostałe liczby znajdują się w zupełnie innych miejscach układu współrzędnych. Jeśli uwierzymy, że sześciany mogą rzeczywiście być elementem brzegu tessaraktu, jak brzeg sześcianu stanowiło sześć płaskich ścian, to wyjdzie na to, że podstawa, którą przed chwilą widzieliśmy całą zaznaczoną na zielono, jest odpowiednikiem krawędzi w sześcianie. Dokładnie to samo obserwował płaszczak, kiedy odkrył, co to jest ściana. To spostrzeżenie przyda nam się bardzo w zrozumieniu Ukrzyżowania… Ale też wiemy już teraz, patrząc na szkic powyżej, że wszystkie osiem wierzchołków małego sześcianu w środku, należałoby je sobie wyobrazić oczywiście nie wewnątrz dużego sześcianu, ale gdzieś w dal osi Z. Prostopadłej równocześnie do wszystkich trzech pozostałych i w związku z tym w rzucie ulegającej tak dziwacznemu skróceniu.

Problem z powyższym szkicem tesseraktu jest również ten, że patrząc nań widzimy – takie jest przemożne wrażenie – jakieś „trzewia”, elementy wewnątrz i na zewnątrz konstrukcji. Musimy tu przede wszystkim uwierzyć, że przestrzenny sześcian może być rzeczywiście brzegiem. Co charakteryzuje brzeg figur i brył zdefiniowanych kostkami ponumerowanymi w sposób, który tu już tak długo analizujemy?

Weźmy najpierw kwadrat. I liczbę 8, która leży na brzegu, a którą wygodniej oznaczyć jako 08; liczbę 19 – również na brzegu; 95 i 40. Porównajmy to z liczbą np. 23, która leży we wnętrzu. Otóż każda z liczb brzegowych charakteryzuje się skrajną wartością jednej z cyfr zapisu. 08 ma minimalną liczbę dziesiątek; 19 – maksymalną liczbę jedności; 95 – maksymalną liczbę dziesiątek; 40 – minimalną liczbę jedności. W narożnikach – wierzchołkach – spotykają się ze sobą dwie skrajne cyfry. We wnętrzu leżą liczby – jak przykładowa 23 – których obie cyfry mają „pośrednie”, a nie skrajne wartości.

Weźmy sześcian – ten zwykły, nie komórkę tesseraktu, choć już płaszczak zauważył wstrząśnięty, że przez jego płaski świat przechodzi być może nieskończoność hiper-światów. 65 zapiszemy teraz jako 065. Ma minimalną liczbę setek, więc należy do brzegu, dokładniej mówiąc, do podstawy. 106 ma minimalną liczbę dziesiątek, więc jest również na brzegu – na pionowej ścianie nad osią X, na której leżą wszystkie takie liczby z zerem w miejscu dziesiątek, np. 207. Wszystkie liczby z 9 w miejscu setek, z 0 w miejscu setek, albo z jakąkolwiek dziewiątką lub jakimkolwiek zerem w którymkolwiek miejscu cyfrowego zapisu należą do brzegu sześcianu.

Z tesseraktem jest dokładnie tak samo. Na szkicu powyżej weźmy dowolny z ośmiu sześcianów zidentyfikowanych wierzchołkami i znajdźmy go, dobierając odpowiednie przekroje na komputerowym modelu. Każda liczba każdego z tych ośmiu sześcianów zawiera jakieś zero lub jakąś dziewiątkę. Każdy z tych sześcianów zlokalizujemy albo wybierając ustawienie domyślne (przekrój według tysięcy), albo wstawiając oś tysięcy na miejsce jednostek, dziesiątek lub tysięcy i wybierając suwakami jedną z dwóch skrajnych pozycji. Robiliśmy to na początku analizy tesseraktu, kiedy niewiele rozumiejąc ograniczyliśmy się do liczenia zaznaczonych kostek brzegu, co pozwoliło nam zidentyfikować objętość wnętrza jako \(8^4\).

Wobec tego wszystkie punkty, wszystkie krawędzie, wszystkie płaszczyzny i wszystkie sześciany, które jesteśmy w stanie wskazać na szkicu powyżej, należą do brzegu tesseraktu, którego struktura jest o rząd wielkości bardziej skomplikowana niż to było z sześcianem.

Czas spróbować powoli włączać wyobraźnię, choć pierwsze próby jej użycia z pewnością jeszcze kilka razy nas zawiodą. W Wikipedii, podobnie jak wielu popularnych filmach pokazuje się tę cytowaną już animację wierzchołków, krawędzi i ścian obracającej się hiperkostki. Animacja mówi więcej niż statyczny obraz, jak ten ze szkicu powyżej. Zmienne w obrocie wielkości niwelują część zafałszowań perspektywy. Animacja pokazana nieprzygotowanym odbiorcom nie wyjaśni jednak niczego, choć autorzy odpowiednich tekstów pokazują ją jako wszystko wyjaśniającą, wyczerpującą ilustrację, a jeśli jej ktoś nie rozumie – trudno. Otóż ta ilustracja nie jest wystarczająca.

Bryła, którą w tutejszym modelu rozważaliśmy jako sztywną konstrukcję związaną z układem współrzędnych – teraz obraca się swobodnie. We własnym "naturalnym środowisku", czyli w czterech wymiarach. My widzimy płaski szkic trójwymiarowego rzutu tej sytuacji. Konstrukcję hipersześcianu rozumiemy już w zasadzie„do cna” po tak długim jej rozważaniu. Mimo to, zakładam, nikt z Czytelników nie jest jej jeszcze w stanie „zobaczyć” na ruchomym szkicu. Wyobraźnia raczej nadal nam przeszkadza.

„I myślę, że musiałby się przyzwyczajać gdyby miał widzieć to, co na górze”

– tak powiada Platon w podobnym kontekście, wkładając tę wypowiedź w usta Sokratesa.

Zapowiadana przygoda jest wciąż przed nami, niezależnie od tego, czy będziemy się przyzwyczajać, czy zrezygnowani machniemy ręką na plastykę wyobrażeń. W rzeczywistości jesteśmy już całkiem blisko finału i rozumiemy więcej niż nam się wydaje.

Kolejny i główny problem szkicu powyżej – animowanego, czy statycznego, to bez różnicy. Gdzie jest wnętrze hipersześcianu? To jest właśnie to pytanie, którego nie znajdziemy w podręcznikach. Ja przynajmniej nie znam takiego, ani też wśród mnóstwa np. filmowych prezentacji, opowiadanych nierzadko przez naukowe sławy, nie spotkałem nikogo, kto by się o tym zająknął. No, to jest kłopotliwe pytanie. I przy okazji powód, który mnie akurat najsilniej przekonał, że Salvador Dali to był malarz prawdziwie genialny. Nie jak Picasso – zaledwie błyskotliwy. Głęboko genialny. Zdolny zajrzeć do wnętrza hipersześcianu.

Patrząc np. na najczęściej spotykany płaski rzut zwykłej trójprzestrzennej kostki, również widzimy na niej narysowane wyłącznie elementy brzegu – sześć płaskich ścian. Niemniej bez trudu wyobrażamy sobie, co jest pomiędzy nimi. Umiemy „włączyć” wrażenie głębi, które znamy z doświadczenia. W szkicu hipersześcianu takiego obszaru zdaje się jednak nie być. Co gorsza, przecież nawet sześcienne hiperściany zdają się na siebie zachodzić i nawet dla nich nie ma miejsca, choć już widzieliśmy, że w rzeczywistości stykają się tylko powierzchnią. Studiując uważnie komputerowy model i udostępniane przezeń przekroje, zobaczymy, że każdy z sześcianów brzegowych, a więc również każdy z ośmiu sześcianów dających się z pewnym trudem zidentyfikować na szkicu, z każdej swojej strony przylega do jakiegoś innego sześcianu brzegowego. Gdzie jest miejsce pomiędzy nimi? No, tak naprawdę patrząc na rzut zwykłego sześcianu również widzimy nachodzące na siebie ściany. Bez trudu jednak potrafimy sobie dodać „głębię” obrazu, czyli brakujący trzeci wymiar. Płaskie kwadraty przylegają do siebie z każdej ze swych płaskich stron. Przestrzenne komórki przylegają do siebie z każdego z sześciu przestrzennych kierunków. Czwartego wymiaru dodać sobie nie potrafimy, bo głębię musielibyśmy umieć postrzegać wzdłuż dwóch niezależnych osi. Z tego powodu nie tylko nie widzimy wnętrza. Na szkicu po prostu go nie ma. Widzimy sklejone ze sobą brzegowe sześciany: pomiędzy sześcianami nie ma miejsca na nic. Z 24 płaskich ścian, jedynie 6 wydaje się być w widoczny sposób „na brzegu”, pozostałe są ewidentnie wewnątrz, choć może nie do końca, co widzimy patrząc na animację. Jak widzimy i na animacji, i na szkicu powyżej, każda ściana każdej z komórek tesseraktu jest równocześnie ścianą innej komórki. Do każdej z sześciu ścian każdej komórki ściśle przylega jakaś inna komórka, a wszystkie razem – jak widzieliśmy – zawierają wyłącznie liczby brzegowe i ani jednej takiej, w której żadna z czterech cyfr nie byłaby ani zerem, ani dziewiątką. Szkic przedstawia zaś również często spotykany model wykonywany z tej okazji z przezroczystych materiałów – ten model jest rzutem hipersześcianu elieminującym jeden z czterech wymiarów. W rzeczywistości, podobnie jak to jest z sześcianem, który ma więcej stron (wymiarów) niż każdy z płaskich kwadratów tworzących jego kształt, tak tesserakt ma o jeden wymiar więcej niż tworzące go sześcienne komórki – a tego wymiaru nie widzimy i nic w tym dziwnego – szkic go nie zawiera, bo i zawrzeć w żaden sposób nie może. Różnica między szkicem sześcianu a szkicem hipersześcianu jest jakościowa. W pierwszym szkicu brakuje jednego wymiaru, który umiemy sobie z łatwością dodać w umyśle. Nawet pozbawiony tej zdolności płaszczak będzie miał nieporównanie łatwiejsze zadanie – w naszym szkicu hipersześcianu brakuje dwóch wymiarów, a sztuczki z perspektywą skracającą dwa wymiary zamiast jednego i nawet ruch całości bardziej nam póki co przeszkadza niż pomaga zrozumieć.

Wykonajmy kolejny myślowy eksperyment i zmieńmy rozmiar naszej bryły. Niech ona teraz obrazuje system trójkowy. Długość krawędzi będzie teraz wynosiła 3, a w notacji używać będziemy cyfr od 0 do 2. Tesserakt będzie miał teraz całkowitą objętość 81, a wnętrze – 1. Jeden będzie zresztą objętością wnętrza każdej hiperkostki o tym rozmiarze w dowolnej ilości wymiarów. Odcinek będzie się składał z liczb 0, 1 i 2 – jedynka oczywiście znajdzie się we wnętrzu. Kwadrat składać się zaś będzie z 9 liczb zapisanych od 00 do 22, a w jego wnętrzu znajdzie się tylko liczba zapisana jako 11 (oznaczające 4); w sześcianie będzie to 111 (oznaczające 13), a hipersześcianie 1111 (czyli 40). Liczba ta będzie przy tym leżeć zawsze na skrzyżowaniu przekątnych: kwadratu, sześcianu i hipersześcianu. Co więcej, w tym samym punkcie krzyżować się będą również środkowe ścian – znów: kwadratu, sześcianu i hipersześcianu.

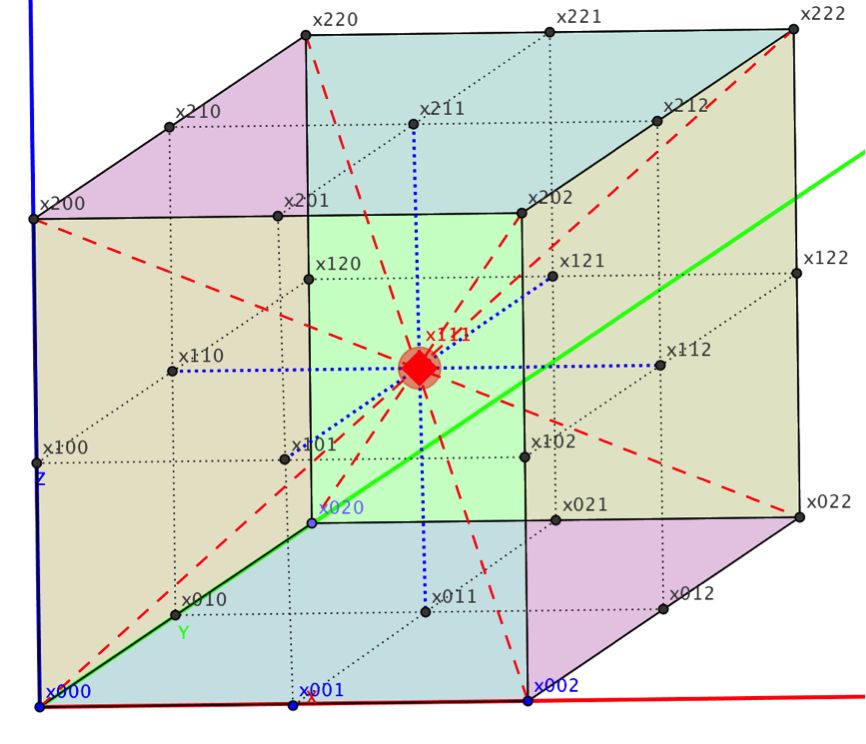
Uważnie przestudiujmy skądinąd prostą sytuację dla sześcianu w trzech wymiarach. Widoczny w środku punkt oznacza poszukiwaną jedyną liczbę wnętrza sześcianu – 111. W odróżnieniu od naszej kostki liczb, nieparzysta długość krawędzi umożliwia znalezienie liczby w środku, ale aż na takiej precyzji wcale nam nie zależy – chcemy po prostu określić, gdzie mogą znajdować się punkty wewnątrz tesseraktu, jeśli chcemy poważnie traktować oferowane nam wizualizacje obracającej się czterowymiarowej bryły. W tej konstrukcji wszystkie inne liczby należą do brzegu sześcianu. Jego wnętrze składa się z jednej tylko liczby – 111. Z tesseraktem będzie podobnie.

Co zrozumiałe, liczba 111 znajduje się w punkcie przecięcia przekątnych. Przekątne w sześcianie znajduje się wg reguł ustalonych jeszcze przez naszego bystrego płaszczaka – łączą one ze sobą liczby, w których wszystkie trzy cyfry zapisu są równocześnie różne. Więc np. 200 i 022, albo 020 i 202. Przekątnych w sześcianie jest cztery. Wszystkie krzyżują się w jednym punkcie. To cecha prostokątnej geometrii foremnej bryły. Z kolei przekątne każdej ze ścian (albo środkowe ich boków zaznaczone tu czarnymi liniami kropkowanymi – co na jedno wychodzi), wyznaczają środki ścian. Proszę się uważnie przyjrzeć liczbom tych środków, żeby dobrze zrozumieć, skąd się tam wzięły, zauważyć ich cechy liczb brzegu bryły itd. Punkt 1111 jest też punktem przecięcia linii łączących środkowe ścian – ale uwaga – tylko tych naprzemianległych. Należy przy tym koniecznie pamiętać, że ściany naprzemianległe to te, które są nawzajem swoim przesunięciem wzdłuż jednej z osi układu współrzędnych. W naszym komputerowym modelu są to przekroje uzyskane przy pomocy tego samego suwaka. W sześcianie o trzech wymiarach tych linii będzie trzy. W hipersześcianie – oczywiście cztery.

Hipersześcian jest również foremny i prostokątny, zatem wszystkie te linie również koniecznie muszą się przeciąć w jednym punkcie. Szukać należy ich w analogiczny do sześcianu sposób.

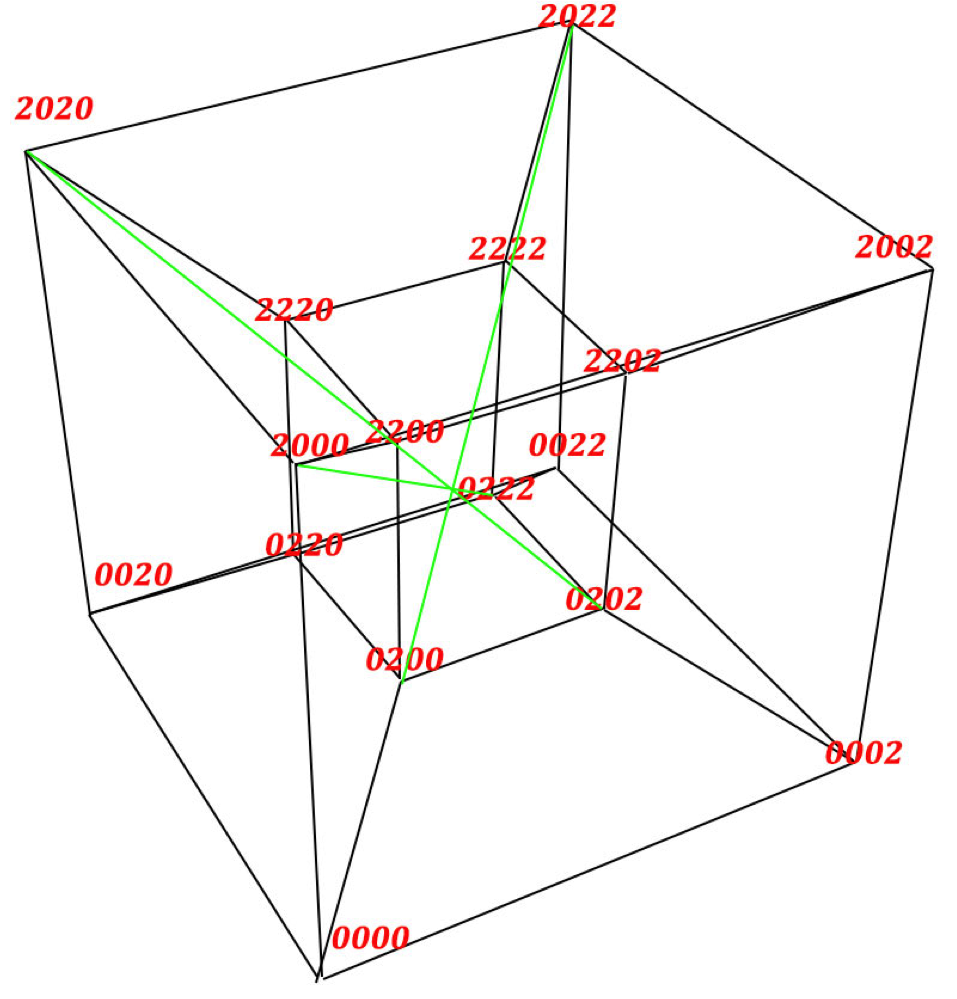
Ów zwykle używany szkic, w rzeczywistości zaś zaledwie rodzaj grafu połączeń wierzchołków hipersześcianu jest pod tym względem skonstruowany sprytnie – odtwarza bowiem cechy foremności bryły.

Przekątnych hipersześcianu jest, jak się należało spodziewać, osiem. Tu zielonymi liniami zaznaczono trzy przykładowe. Czytając niniejsze warto samodzielnie spróbować zlokalizować pozostałe, co również wymaga wysiłku. Przy takiej postaci szkicu jednak – rzeczywiście wszystkie przekątne przetną się w jednym punkcie i ten punt widzimy.

Zamiast środków ścian sześcianu, które połączone (łączyliśmy ściany naprzemianległe) również wyznaczały nam środek bryły, trzeba by teraz połączyć środki naprzemianległych komórek. Nie ma tego na rysunku – już zwykły sześcian zamienił się nam od tych wszystkich linii w mało czytelną plątaninę – ale widać po pierwsze, że naprzemianległe komórki identyfikujemy tu z łatwością dokładnie jak naprzemianległe ściany, bo one po prostu leżą naprzeciw siebie; po drugie, że odpowiednie środkowe także przetną się w jednym punkcie. Bryła jest symetryczna. No, właśnie na tym polega fałsz szkicu, a dokładniej naszego automatycznego odbioru. Widzimy tylko trzy płaszczyzny tej symetrii, jak w „zwykłej przestrzeni” – a powinniśmy widzieć cztery, czego w zwykły sposób zobaczyć się nie da. Ruch animacji – obawiam się bardzo – póki co wyłącznie zaciemnia obraz sytuacji, zamiast ją wyjaśniać.

Widzimy jednak choćby to, że linie przecinają się we wnętrzu środkowej komórki. A to jest krawędź – w jej wnętrzu, jak widzieliśmy dowodnie, znajdują się wyłącznie liczby brzegu. Liczba 1111 – choć widzimy ją we wnętrzu „centralnej komórki”, nie może do niej należeć. Możemy z łatwością wymienić – patrząc na wierzchołki komórki – listę wszystkich zawartych w niej 27 liczb (m.in. po to zredukowaliśmy rozmiar całości). Niech będzie, wymieńmy: 0200, 0201, 0202, 0210, 0211, 0212, 0220, 0221, 0222 . Mamy za sobą 9 liczb kwadratu podstawy i przechodzimy do środkowej warstwy: 1200, 1201, 1202 – pierwszy rząd w tej warstwie, teraz drugi: 1210, 1211, 1212. Możemy przerwać – liczba 1211, a nie 1111 znajduje się w środku przeszukiwanej komórki. Liczby 1111 na tym szkicu nie widać. Jest w rzeczywistości pomiędzy wszystkimi widocznymi tu sześciennymi komórkami tesseraktu. Gdzie tu jest coś "pomiędzy"? Takiego miejsca tu w ogóle nie ma! Nie znajdziemy go również we wspomnianym przestrzennym modelu, gdybyśmy go trzymali w ręku. Proszę spróbować postawić hipotezę – pomiędzy którymi widocznymi ośmioma komórkami leży liczba 1111? To ciekawe doświadczenie. Liczbę 1111 powinniśmy móc zlokalizować wybierając odpowiednie cztery współrzędne, więc da się do zrobić posługując się krawędziami hiperkostki – każda z nich równoległa do którejś współrzędnej, co już raz wyżej zaznaczaliśmy na szkicu kolorowymi strzałkami. Każda hipoteza – proszę je naprawdę postawić, bo to kształcące – doprowadzi do sprzeczności, jakby liczba 1111 musiała istnieć w wielu miejscach na raz, a równocześnie w żadnym z nich nie mogła istnieć w pełni. Sprzeczność sugerowałaby niemożliwość konstrukcji, a jednak w rzeczywistości konstrukcja ta istnieje – istnieje system dziesiętny liczb, a w nim hipersześcian pierwszych 10 tysięcy oraz wszystkie następne hiperbryły aż do nieskończoności – i istnieje w tych bryłach najzwyklejsza arytmetyka oraz równie zwykła geometria. Istnieją liczby w środku każdej takiej hiperkostki. Co więcej, ten niemożliwy szkic rzutu jest geometrycznie najzupełniej poprawny. To zwykły rzut perspektywiczny. No, kosmiczna świadomość pełną gębą… Otóż liczba 1111 oczywiście istnieje w miejscu oznaczonym przez przecięcie zielonych linii. Jednocześnie jednak jest gdzieś zupełnie indziej niż liczba 1211, którą tam zlokalizowaliśmy. No, trzeba by się „cofnąć o setkę”. Ale w którą stronę? Do wyboru mamy 6 stron wzdłuż trzech osi – żadna z nich na tym szkicu nie jest tą właściwą! To ją trzeba sobie wyobrazić. Już ją zresztą oznaczaliśmy powyżej – niebieską strzałką setek, która rozmnożyła się do kilku wskazujących przeciwne (prostopadłe) kierunki. Szukamy 1111, która jest jedyną liczbą wnętrza tak skosntruowanego tesseraktu. I jedyną, której nie ma na tym szkicu!

W rzeczywistości ona się po prostu pokryła w rzucie z liczbą 1211, którą zlokalizowaliśmy wewnątrz mniejszej kostki.

Wracając do hiperkostki liczb o rozmiarze 10, a nie 3. Możemy z łatwością wymienić liczby leżące na przekątnej. Wybierzmy najłatwiejszą do tego celu – tę zaczynającą się od 0. Następną liczbą będzie 1111, potem 2222, 3333 itd. aż to 9999. Z wyjątkiem pierwszej i ostatniej wszystkie pozostałe należą do wnętrza hiperkostki i żadnej z nich nie ma w żadnej z ośmiu brzegowych komórek tesseraktu. Jaki kształt ma wnętrze tesseraktu? To proste – jest tesseraktem. To wyjaśnienie podaję złośliwie, ponieważ chodzi o tesserakt, którego na szkicu nie ma. W naszym komputerowym modelu da się go zobaczyć całkiem po prostu – choć nigdy w pełnej krasie. Ona się może dopiero objawić myślom – nie oczom.

Powiedzieliśmy również, że skoro w sześcianie da się narysować trzy środkowe łączące pary naprzemianległych ścian, w hipersześcianie takich środkowych – łączących tym razem komórki – powinno być cztery. Patrząc na powyższy szkic widzimy tylko trzy. Czwarta zredukowała nam się do punktu. Czwarta środkowa łączy bowiem jedyne dwie komórki, które kształtem przypominają nam sześciany zwykle rysowane. Tę „zewnętrzną” i tę „środkową”. W rzeczywistości jedna powinna przesłaniać drugą, zamiast ją zawierać – patrzymy najwyraźniej wzdłuż jednej z czterech osi układu współrzędnych – równoległej do tej środkowej. Nawet wiemy do której – to jest właśnie oś setek, ponieważ właśnie setkami różnią się te dwie komórki i to dlatego liczby 1111 nie mogliśmy nigdzie zlokalizować. Proszę więc jeszcze raz spojrzeć, w jaki sposób pomiędzy wierzchołkami większego sześcianu, a odpowiadającymi im wierzchołkami tego mniejszego rosną liczby setek. To przecież jeden z czterech wymiarów hiperprzestrzeni. Na szkicu – w wersji z kolorowymi strzałkami oznaczającymi cztery kierunki hiperświata widać, że wzrost od naprzemianległych wierzchołków następuje w przeciwnych kierunkach!

Nie jest to bynajmniej tak absurdalne, jak się na pierwszy, drugi i nawet trzeci rzut oka wydaje. Trzeba to, co widzimy, próbować rozumieć z rozmaitych perspektyw – nie zawsze odpowiada to perspektywom spojrzeń, bo tu możliwości mamy ograniczone.

Płaski wizerunek obracającej się hiperkostki oglądany w okularach do stereoskopowej projekcji powinien dać obraz zgodny z obrazem "sześcianu w sześcianie". To jest bowiem najzupełniej prawidłowy rzut hipersześcianu na przestrzeń trójwymiarową – rzut perspektywiczny. Rzut sześcianu na płaszczyznę wykonany z podobnej perspektywy dałby obraz "kwadratu w kwadracie". Rzutujemy z punktu ponad "dachem" tesseraktu na "hiperpłaszczyznę" równoległą do podstawy. Okulary "4D" powinniśmy raczej mieć na sobie oglądając przez nie wykonany np. z pleksi model "sześcianu w sześcianie". Okulary musiałyby pokazywać "głębię" równoległą do czwartego wymiaru, a tego się zrobić nie da. Ciekawa jest natomiast w tej sytuacji wizja „wywracania na lewą stronę” (efekt obrotu wokół osi, których nie da się skonstruować w trójprzestrzeni) i „wchłaniania” jednej komórki przez drugą (efekt braku osi odpowiedniej perspektywy). Z naszym "modelem z pleksi" niczego już nie robimy, przedstawiając go na animacji pokazującej obrót. Obrót odbywa się w 4D, zatem nasz rzut wymodelowany z pleksi wywija nam się dokładnie tak, jak to widzimy. Patrząc więc na obracający się płaski schemat brzegu bryły, należy zatem próbować śledzić w myślach również skonstruowane przed chwilą przekątne i (lub) środkowe. Oraz strzałki pokazujące osie jednostek, dziesiątek, setek i tysięcy. Jeśli jesteśmy je w stanie „zobaczyć”, widzimy tesserakt w jego prawdziwej postaci i wiemy, że on się po prostu obraca, a nie wywija na lewą stronę. To właśnie na tym polega tu sztuka „widzenia”.

Animacja obok pokazuje zielonym kolorem główne przekątne tesseraktu.  W każdej fazie obrotu przecinają się prawidłowo. Widzimy teraz, że tak wyznaczony środek "przepływa" z komórki do komórki, choć w żadnej z nich nie może się zawierać, o czym już wiemy. Czerwone linie są z kolei przekątnymi sześciennych komórek brzegowych i wyznaczją ich środki. To są przeciwległe komórki. W widocznym tu obrocie co drugi moment, w którym przecięcia czerwonych przekątnych nachodzą na siebie jest tym momentem, w którym jedna z naprzemianległych komórek "wchłania" drugą. Wybrane komórki są owym zewnętrzym i wewnętrznym sześcianem widocznym na statycznym szkicu. Żółta linia łaczy środki naprzemianległych hiperścian i zgodnie z przewidywaniami przechodzi przez środek hiperkostki. Na tej animacji wnętrza nie widzimy nadal. A jednak dość wyraźnie widać, że hiperściany krążą wokół środka, a odległość między nimi pozwala myśleć o istnieniu wnętrza bryły. Trzeba tej animacji przyjrzeć się przez jakiś czas, żeby to dostrzec. Da się wtedy również zobaczyć, że wzajemne "wchłanianie" komórek jest następstwem właśnie obrotów.

Szkic, który próbujemy zrozumieć, staje się w ten sposób po raz pierwszy sytuacją, w której możemy się poczuć lepiej niż płaszczak, kiedy sobie próbuje wyobrazić sześcian.  Płaszak bowiem nie obserwowałby wcale dwóch wchłaniających się naprzemian kwadratów. Ich istnienie obserwowałby w powstaci punktów poruszających się w jednej linii. Zagadka nie do rozwikłania w porównaniu z naszą.

Cokolwiek niejasne pozostaje prawdopodobnie nadal pojęcie przestrzennego rzutu, na którego wizerunek patrzymy. Komputerowy model, z którego tu korzystaliśmy, pokazuje na ogół przekroje – po to został skonstruowany. Przekrój, który jest sześcianem już rozumiemy. Ustalamy więc np. wartość tysięcy na 5 i widzimy liczby od 5000 do 5999 ułożone w sześcian. Rzut wzdłuż osi tysięcy (prostopadły, więc prostszy niż powyższy i przez to nieco mniej obrazowy) jest czymś innym. Widzimy znów sześcian, a w nim oprócz 0 również liczbę 1000, 2000, 3000 itd. -- wszystkie w jednym miejscu. Nad zerem widzimy 100, 1100 itd. Przykład możemy zobaczyć w domyślnym widoku, odhaczając zaznaczoną domyślnie opcję "przekrój wg T". Kostki sześcianu stracą wówczas przezroczystość (skoro na miejscu każdej pojawi się 10 równocześnie) i niewiele zobaczymy. Jeśli jednak wybierzemy teraz opcję "ukryj" znikną nam wszystkie kostki z wyjątkiem tych podzielnych przez 9. Zobaczymy czerwony sześcian. Manipulując suwakiem po prawej stronie możemy sobie kazać pokazać wielokrotności innych liczb z przedziału do 10 tys. Wielokrotności 11 utworzą w rzucie sześcian ze szczeliną po przekątnej. Niektóre inne liczby dają ciekawe wzory.

Pomocne jest również pamiętać o jeszcze kolejnej własności brył w dowolnej ilości wymiarów. Rodzina rozważanych tu sześcianów (poczynając od odcinka, a na skromnym tesserakcie kończąc) to bryły foremne, co między innymi oznacza ich wypukłość. W takiej bryle z każdego wierzchołka widać wszystkie pozostałe. I równocześnie wszystkie inne „elementy konstrukcyjne”. Nie inaczej jest w hipersześcianie. I to jest kolejna zafałszowana cecha oglądanych tu szkiców nawet w ich animowanej wersji. Patrząc z czwartego wymiaru nie widzimy zasłaniania niczego przez żadną z komórek brzegu. Przeciwnie – w rzeczywistości widzimy równocześnie każde osiem wierzchołków każdej komórki.

Jeszcze więcej – żyjąc w czterowymiarowej przestrzeni i patrząc na umieszczony w niej trójwymiarowy sześcian, patrzymy nań zawsze z góry – no, chyba, że postanowimy stanąć „na jego poziomie”, jak żółty kwadrat stał na poziomie gwiaździstej strażniczki. Patrzenie z góry dodatkowego wymiaru ma zawsze tę samą własność „rentgenowską” – widzimy sześcian ze wszystkich stron równocześnie: wszystkie sześć jego ścian. Podobnie jak w niepojęty dla płaszczaka sposób my widzimy wszystkie cztery boku kwadratu. To jest również skutek tego, że czwarta oś współrzędnych jest równocześnie prostopadła do wszystkich trzech pozostałych.

Tę ostatnią cechę nadprzestrzeni wykorzystywał świadomie Picasso, dowiedziawszy się o niej z lektury Poincarego. Słynne portrety Dory Maar pokazują więc np. twarz z profilu i en face równocześnie, co jest Picassa odkryciem w kubizmie. Podobny zabieg stosowano jeszcze w Lascaux, w Mezopotamii i Egipcie (według mnie w Lascaux z najlepszym i naprawdę świetnym skutkiem dla dramatyzmu przedstawień). Podobnie często rysują dzieci. Być może jest w tym jakaś intuicja i może obcowanie z Picassem jest w stanie te intuicje rozwinąć, choć sądzę, że to jest raczej właśnie taka „perspektywa dziecięca”, która wymaga dodatkowego wysiłku w ogadnięciu intencji autora co do rozmieszczenia w przestrzeni przedstawionych na rysnku obiektów.

Działa teraz lepiej, prawda? Lepiej, nie lepiej – zakładam, że Czytelnik nadal „nie widzi”. To zrozumiałe. Warto wiedzieć, że zobaczyć naprawdę po prostu się nie da, podobnie jak płaszczak, którego wzrok obejmuje wyłącznie linie przekrojów, nigdy nie zobaczy kwadratu, choć go dobrze rozumie, a my tu wymagamy zobaczenia przezeń sześcianu. Ale już teraz rozumiemy raczej wszystko w konstrukcji hipersześcianu. Pozostaje, zgodnie z sugestią Platona, zacząć się przyzwyczajać. Przed nami ten wgląd w przestrzeń komputerowego modelu, który jakiś rodzaj widzenia zapewni, choć trudno powiedzieć, jak szybko i ile doświadczeń będzie trzeba zebrać.

„Widzenie”, o którym mowa w odniesieniu do obracającego się szkicu, może mieć oczywiście jedynie intuicyjny charakter, choć dostarcza euforii zrozumienia. Narysować się tego nie da. Ani wyrzeźbić w przestrzeni. Prawdę, jak powiedzieliśmy, pokazuje nie szkic powyżej, ale logika trójwymiarowych przekrojów czterowymiarowej bryły. Jeśli więc ktokolwiek twierdzi, że w szkicu widzi tesserakt plastycznie – konfabuluje.

Chyba, że patrzącym jest Salvador Dali, który potrafił użyć niezwykle głębokiej przenośni i – jak to się najwyraźniej często zdarza – ta jego przenośnia okazuje się przez to płodna filozoficznie, albo – jeśli wola – teologicznie.

Jeszcze jedna zatem komputerowa eksploracja przed przeglądem malarstwa. Trzeba w końcu wreszcie obejrzeć wnętrze hipersześcianu. I zrozumieć, na czym polega siatka hipersześcianu, bo to ją właśnie uwiecznił Dali w swojej teologicznie przenikliwej (choć może tylko przypadkiem) wizji Ukrzyżowania, wobec której kubistyczne gry Picassa nie wytrzymują moim zdaniem porównania -- intelektualnie, bo o estetyce nie śmiem się wypowiadać.

Przypomnijmy sobie najpierw płaszczaka i jego eksplorację brzegów sześcianu. Manipulując przekrojami i zaznaczeniami, jak to zrobimy my za chwilę, płaszczak zauważył w jaki sposób stykają się ze sobą kwadratowe, płaskie ściany sześcianu. Zobaczył, że ściany te mają w sąsiednich parach wspólne krawędzie. Potrafił więc zbudować we własnym płaskim świecie schemat konstrukcyjny sześcianu. To oczywiście nie jest jedyna możliwa wersja, niemniej równie oczywiście kwadratów nie da się ułożyć w siatkę w sposób dowolny. Np. nie miałaby sensu siatka, w której kwadraty leżą w jednej linii – sześcianu nie dałoby się z tego złożyć. Co więcej, składanie tej siatki w sześcian – dla nas banalne – dla płaszczaka byłoby znów przeżyciem o iluminacyjnym charakterze. Zagięcie w górę ramion widocznego tu krzyża oznaczałoby ich natychmiastowe zniknięcie z płaskiego świata. Płaszczak sądził dotąd, że obroty odbywają się wokół punktu na płaszczyźnie. Teraz odkrył, że w rzeczywistości obroty odbywają się wokół liniowych osi i w dodatku te obroty, które dobrze zna z płaskiego doświadczenia, w rzeczywistości odbywają się wkoło osi hiperprzestrzennej. Obolałemu już bardzo, jak sądzę, Czytelnikowi darujemy rozważania konsekwencji tego odkrycia dla czterowymiarowej przestrzeni. Spytajmy tylko, gdzie jest wnętrze sześcianu w takim widoku?

Sama operacja zwijania siatki jest z punktu widzenia płaszczaka niezwykle skomplikowanych procesem. Nie inaczej jest w naszym przypadku, a poziom komplikacji jest tu o rząd wielkości większy. Zgodnie z obietnicą, szczegóły sobie tu darujemy.

Zaglądać do wnętrza hipersześcianu będziemy jednak w ten sposób, że najpierw oznaczymy brzegi, co już raz robiliśmy, a robiąc to tym razem, warto przy okazji zwrócić uwagę na wartości liczb pojawiających się na wspólnych krawędziach brzegu, by nabrać wyobrażenia o możliwej konstrukcji siatki.

Oznaczmy więc w naszym modelu sześcienne komórki brzegu hipersześcianu. Najpierw więc zobaczmy domyślny widok. Zaznaczony jest przekrój według T = 0. Widzimy pierwszy tysiąc liczb. Zaznaczamy je. Przesuwamy suwak na T = 9, widząc teraz ostatni tysiąc kolejnych liczb i zaznaczamy je również.

Tu uwaga – nie ulegajmy łatwym złudzeniom. Kolejne tysiące nie wyłaniają się „z głębi” tego, na co patrzymy. Możemy sobie zmienić perspektywę i obraz będzie wyglądał tak samo, a quasi-symetryczne (równocześnie hiper-symetryczne: z każdego kierunku zobaczymy to samo) ułożenie czerwonych wielokrotności dziewiątek jeszcze to wrażenie podkreśli. W czteroprzestrzeni nie mamy do czynienia z kostkami ułożonymi jedna za lub jedna nad drugą. Tysiące układają się według czwartego wymiaru i pojawiają się „znikąd” – z kierunku prostopadłego do wszystkich trzech, które teraz widzimy.

W lewej górnej części wybieramy teraz opcję „tysiące zamiast jednostek”. U dołu aktywny jest przekrój według X = 0. Widzimy kostkę, w której dwie naprzemianległe ściany są już zaznaczone. Domyślamy się, że to są ściany styku z dwiema zaznaczonymi wcześniej komórkami pierwszego i ostatniego tysiąca liczb. Wyświetlmy wartości.

Istotnie lewa z tych ścian (patrząc tak, że czerwona oś X zwrócona jest w prawo) zawiera liczby z pierwszego tysiąca, a prawa z ostatniego. Zielone ściany widocznego tu sześcianu są oczywiście płaskie – bo są podwójnymi przekrojami. Oba przekroje mają jedną zmienną – jednostki – ustaloną na tę samą wartość 0. Druga ze zmiennych – tysiące – jest ustawiona na 0 z lewej i na 9 z prawej strony.

Każda z 800 widocznych tu niezaznaczonych liczb leży w tesserakcie pomiędzy brzegową komórką pierwszego i ostatniego tysiąca – jeśli patrzeć wzdłuż osi jednostek. Skoro tak, to – próbując sobie wyobrazić sytuację – musi to dotyczyć wszystkich innych liczb dotąd niezaznaczonych. Patrzymy przecież prostopadle do osi tysięcy. Sprawdźmy, przesuwając suwakiem przekrój według X. X = 1 pokazuje nam ten sam układ, ale wszystkie liczby mają teraz 1, a nie 0 w miejscu jednostek. Wszystkie 10 takich sześcianów oglądanych od X = 0 do 9 ma tę samą lewą i prawą ścianę zaznaczoną na zielono. Wzdłuż tego kierunku zatem wszystkie 8000 liczb poza 2000 zaznaczonych leży pomiędzy pierwszym i ostatnim tysiącem. Arytmetycznie jest to truizm przecież: oglądamy liczby od 1000 do 8999, to jasne, że są większe od pierwszego i mniejsze od ostatniego tysiąca. Zaznaczmy brzegowe komórki w tym przekroju – dla X = 0 i 9.

Mamy w ten sposób zaznaczone 3600 liczb w czterech komórkach brzegowych, przylegających do siebie parami, a parami naprzemianległych. 4 sześciany po 1000, i 4 ściany po 100 wspólne.

Idźmy dalej. Odznaczamy poprzednie opcje i wybieramy następną – tysiące zamiast dziesiątek. Patrzymy teraz wzdłuż tej osi, a ona jest prostopadła w stosunku do obu poprzednio wybranych. Jak należy się podziewać, każdy sześcian ma teraz w związku z tym cztery ściany oznaczone na zielono. Sąsiaduje z naprzemianległymi komórkami skrajnych wartości tysięcy i skrajnych wartości jednostek. Dzieje się tak wzdłuż całej osi dziesiątek – dla wszystkich dających się tu wybrać wartości. Zaznaczamy skrajne komórki wzdłuż tej osi.

Tysiące zamiast setek – ten przekrój pokazuje sytuację dotąd niewidzianą. Nie ma oczywiście niczego wyjątkowego akurat w tej, niebieskiej osi układu współrzędnych – jest po prostu czwartą wybraną w kolejności. Widzimy zawsze sześcian, a wszystkie trzy kierunki zostały już wcześniej wybrane i podwójnie oznaczone dla każdej ze ścian. Wszystkie ściany są i muszą być zaznaczone. Jeśli trzeba, wlatujemy do środka, albo definiujemy sobie płaski przekrój, ale oczywiście wiemy, że w środku nic nie jest zaznaczone i tak jest wzdłuż wszystkich wartości setek. Cały nasz sześcian widoczny w widoku Z = 0 ma dla wszystkich liczb na wszystkich zewnętrznych ścianach po dwie skrajne wartości. Na każdej ścianie jest 0 w miejscu setek i 0 lub 9 dla którejś pozostałej. Zaznaczamy obie skrajne wartości w tym przekroju.

Pamiętajmy przez cały czas, że gdybyśmy mogli naprawdę „zajrzeć” do czterowymiarowej przestrzeni, widzielibyśmy z tej perspektywy obraz pozostałych trzech, a nie tylko dwóch osi równocześnie, ponieważ wszystkie trzy byłyby prostopadłe do kierunku naszego wzroku.

Czytelnikom pozostawiam samodzielne próby zidentyfikowania poprawnych i niepoprawnych sposobów łączenia sześciennych komórek w siatkę, z której da się złożyć tesserakt. Da się to zrobić identyfikując, co powinno się z czym stykać w tesserakcie tak, by np. dwa sześciany siatki nie trafiły po zwinięciu w to samo miejsce czteroprzestrzeni, jak to się również może zdarzyć przy próbach złożenia nieprawidłowej siatki sześcianu. Powyższy proces oznaczania komórek brzegowych i obserwowania ścian Czytelnik powinien kilkakrotnie powtórzyć samodzielnie, eksperymentując i uważnie obserwując zaznaczane pary. Warto również próbować w różnych przekrojach obserwować wnętrza, konstruując w nich np. samodzielnie zaprojektowane kształty (pamiętajmy, że złożenie czterech przekrojów pokaże nam pojedynczą liczbę, więc skonstruować da się tu wszystko). Choćby ośmioramienny krzyż oczywiście możliwy w czterech wymiarach, a niemożliwy w trzech – możemy ramiona „zaznaczyć” nadając im różne długości. Wreszcie trzeba pomyśleć o tym, jak dokładnie i wokół których osi należałoby obrócić elementy siatki tesseraktu, by się wszystkie znalazły położone wzdłuż trzech, a nie czterech wymiarów i by dało się je zobaczyć w naszym świecie. Jednym z kluczowych momentów jest właśnie oglądane przed chwilą konsekwencje wybrania czwartej osi. W jaki sposób osiem sześciennych obiektów potrafi zamknąć osiem „końców” ograniczonej czterowymiarowej przestrzeni? To „skrzyżowanie” siatki, wyjaśnia również zresztą ów dziwnie wyglądający moment animacji, na którym „mniejszy” sześcian „wewnętrzny” zostaje „wchłonięty” przez „większy”, który w trakcie wchłaniania „rośnie” i „wywija się na lewą stronę”, by móc się zetknąć z sześcianami odstającymi odeń wzdłuż czwartego kierunku. Próby zrozumienia tego ułożenia nie wymagają już żadnych nowych informacji.

Możemy teraz przekroje wybrać ponownie. W każdym z nich zobaczymy oczywiście ten sam obraz sytuacji, wyglądający zresztą co do samej tylko ilości wymiarów identycznie, jak obraz zwykłego sześcianu, którego ściany oznaczymy na zielono stosując identyczną metodę w świecie płaszczaka.

Tam – patrząc wzdłuż jednej z trzech osi widzieliśmy zawsze kwadrat. Był albo cały zielony – dla skrajnych wartości wzdłuż osi patrzenia – albo był przekrojem wewnętrznym. Jego wszystkie cztery brzegi były wtedy zaznaczone, podczas, gdy wnętrze przekroju – fragment wnętrza sześcianu – pozostawał niezaznaczony. Cała tajemnica polegała na patrzeniu z jednej strony – przy pomocy ortogonalnych rzutów według osi równoległych do wybranych osi układu współrzędnych. W tej sytuacji wierzchołki sześcianu pokrywają się według rozróżnialnych współrzędnych prostopadłych do kierunku patrzenia (X i Y, jeśli patrzymy wzdłuż Z) i widzimy kwadrat. W czteroprzestrzeni patrząc podobnie ortogonalnie jesteśmy w stanie rozróżnić 8 z 16 wierzchołków, ponieważ one pokrywają się parami. Widzimy podobnie – zależnie od „głębokości przekroju”, albo sześcian brzegowy, albo przylegające do brzegów sześcienne przekroje wnętrza.

Z dostępnej w wizualizacji opcji 4D powinniśmy skorzystać pod koniec tej dość trudnej zabawy, kiedy już rozumiemy konstrukcję dobrze, ale szkic wciąż wymyka się intuicyjnemu zrozumieniu. Prawdopodobnie to jest dobry moment.

Opcja 4D zawiera dwa widoki ustawiane przy pomocy opcji "Przekrój / Rzut" widocznej w lewym górnym narożniku okna. Opcja "Przekrój" jest w zasadzie nierozróżnialna od prostopadłego rzutu wzdłuż osi T. Widzieliśmy podobne przedstawienia na poziomie "3D", gdzie dodatkowo mogliśmy korzystać z niedostępnej tu opcji zamiany współrzędnych. Dodatkowo z prawej strony widzimy dwa suwaki obrotów wokół osi Y i Z. Umieszczona powyżej nich opcja "Uruchom" włącza animację obrotu wokół osi Z. Uwaga – to jest zwykły obrót w trójwymiarowej przestrzeni. Obracamy rezultat rzutowania lub rezultat przekroju. Widzimy zwykłą kostkę w trzech wymiarach.

Opcja "Rzut" pokazuje rzeczywistość szkicu, który w statycznej lub animowanej postaci był przedmiotem dotychczasowych dociekań. Widzimy wszystkie 10 tys. liczb. Niestety również stosunkowo silne komputery mają tu kłopot z przedstawieniem sytuacji – obroty i animacje dobrze działają na przekrojach zawierających np. 1000 liczb komórek brzegu, wybrane krawędzie, przekątne itd.

Osi, a właściwie płaszczyzn obrotu jest tym razem 6. To kolejny kłopotliwy problem – niezgodny z trójwymiarowymi intuicjami. Zrozumiały jest w każdym razie obrót w płaszczyźnie. Trójwymiarowy obrót wokół Z jest obrotem wzdłuż płaszczyzny XY. Trzy suwaki u góry dotyczą płaszczyzn niezawierających osi T – każda z nich jest do niej prostopadła, będąc równocześnie prostopadłą do którejś ze "zwykłych" osi: Z w przypadku obrotu w płaszczyźnie XY; Y w przypadku obrotu XZ itd. Sytuacja jest zrozumiała, kiedy posłużymy się jakimś przekrojem (np. wzdłuż osi dziesiątek – Y=0) i skorzystamy z suwaków obrotu z górnego rzędu. Zobaczymy normalny, trójwymiarowy obrót.

Zmieni się to radykalnie po skorzystaniu z suwaków z dolnego rzędu. Każda z płaszczyzn obrotu zawiera tu oś T, a to wzdłuż tej osi odbywa się rzutowanie 10 tys. liczb tworzących tesserakt. Cała kostka i wszystkie jej komórki oraz przekroje zaczną się wyginać tak dziwacznie, jak to dotąd oglądaliśmy na animowanym szkicu. Opcja "Uruchom" włączy teraz animację obrotu w płaszczyźnie XT. Zastosowane tu obroty są elementarnymi przekształceniami macierzowymi, a wyjaśnienie tej algebry oraz geometrii zostanie omówione osobno w innym dziale (w tekstach pojawiają się linki). Technika rzutowania (nie omawiam jej tu, ponieważ również to zagadnienie powinno się doczekać osobnego opracowania) jest trywialną konsekwencją wzajemnej prostopadłości wrzystkich trzech wymiarów. To rodzaj "cienia", w którym źródło światła jest umieszczone na niewidocznej tu osi T (prostopadłej do wszystkich trzech postałych osi) ponad hipersześcianem. Grupy punktów hipersześcianu, które są bliżej "źródła światła", rzucają cień większy od tych bardziej oddalonych, czym rządzi zwykłe podobieństwo trójkątów. Suwak u góry okna umożliwia zmianę położenia środka projekcji. Przesunięcie go do skrajnej prawej pozycji umieszcza środek projekcji na wysokości T = 100, przy długości krawędzi hiperkostki 10, co oznacza praktycznie ortogonalną projekcję i hipersześcian staje się widoczny jak zwykła kostka.

Zrozumienie zagadnień tutaj centralnych, a zatem problemu wnętrza i jego widoczności w rzucie oraz sensu obrotów w hipersprzestrzeni stanie się najzupełniej możliwe przy eskperymentowaniu z dostępnymi tutaj przekrojami, obratami i zaznaczeniami.

Rozwinąwszy siatkę sześcianu płaszczak zastanawiający się, jak wyobrazić sobie miejsce, w którym powinno być wnętrze, musiałby i tak zobaczyć niemożliwy do zobaczenia trzeci wymiar, bo oczywiście dla nas, a nieoczywiście dla płaszczaka, wnętrze musiałoby unosić się ponad kwadratami siatki, na przykład tak, jak to jest tu widoczne.

W naszym czteroprzestrzennym przypadku sześciany zajmują miejsce kwadratów w każdym z czterech możliwych kierunków patrzenia. Dla skrajnych wartości zobaczymy więc zawsze komórkę tesseraktu wypełnioną w całości zielonym zaznaczeniem. Dla każdej wartości pośredniej zobaczymy – uwaga – trójprzestrzenny przekrój tesseraktu o wymiarach 8 x 8 x 8 x 8 z liczbami o cyfrach z przedziału od 1 do 8. W czterech wymiarach zobaczylibyśmy go z jednej strony, mając drugą zasłoniętą. Patrząc z piątego wymiaru widzielibyśmy go z każdej strony, jak z samczej lub artystycznej wyższości spoglądał szowinistycznie na Dorę Maar Pablo Picasso. Ale my patrzymy z trójwymiarowej perspektywy, więc podobnie, jak płaszczak domyśla się tajemnicy ponad siatką kwadratów, które jako jedyne jest w stanie zrozumieć, tak my kontemplujemy siatkę sześcianów – jedyny namacalny fragment hiperrzeczywistości, który możemy zobaczyć w trzech wymiarach.

Spójrzmy na dzieło Dalego zatem.

Widzimy intuicję zdumiewającą. Próbując patrzeć ściśle – jeśli Chrystus tu przedstawiony ma pochodzić z wnętrza nadziemskiej bryły, być jej częścią, istotą, czy czymkolwiek, powinien znajdować się w jakiejś „chmurze” dookoła krzyża. Ale przecież On nie całe wnętrze musi wypełniać. Tak czy owak, jest częścią nadrzeczywistości, wnętrza ograniczonego rozwiniętą teraz siatką krzyża, więc np. już gwoździe nawet Go nie dotykają, bo tego rodzaju dosłowność przestrzennych relacji trzech wymiarów w nadprzestrzeni nie ma sensu. Co prawda jakiekolwiek dwa byty zajmują to samo miejsce w trzech lub czterech wymiarach, jeśli będą one widoczne na przekroju dwu lub trójwymiarowym – koniecznie również się w nim pokryją. Ale nie każdy cień tych bytów – choć widać je na nim w jednym miejscu – oznacza, że one rzeczywiście się pokrywają w przestrzeni. Gwoździe być może przebiją Chrystusa w rzucie… Możemy się tego domyślać tylko.

Ten obraz może być przypadkowym efektem podobieństwa siatki do krzyża. Mogło być tak, że zobaczywszy krzyż Dali w zwykłym kaprysie po prostu domalował na nim „brakującego” Chrystusa, wiedząc tyle, że czwarty wymiar sugeruje głębię w jakiś sposób niepojętą. Ale przecież siatkę zwykłego sześcianu też się tak przedstawia. No, mógł się Dali zafascynować czyjąś opowieścią o wyższych wymiarach, jak Picassa zafascynował wykład Poincarego. Ale właśnie te zawieszone w przestrzeni gwoździe są w tym obrazie – niezwykle zresztą oszczędnym w tej „nieziemskiej” części i w tej oszczędności przypominającym ikonę bardziej niż zachodni realizm – symbolem zrozumienia znaczeń odmiennych perspektyw czterowymiarowego świata…

Można też po prostu zobaczyć tu Chrystusa zstępującego z czterech wymiarów – z nadrzeczywistości. Z zaświatów. Kogoś nieziemskiego. Patrzymy nie mogąc Go nigdy w pełni objąć ani myślą, ani wzrokiem. To narzucająca się i najbardziej oczywista interpretacja. No, i oczywiście to nie jest przedstawienie matematycznie poprawne. Ponad krzyżem – siatką nie zobaczymy przecież żadnego czterowymiarowego obiektu, tu wolno umieścić wyłącznie symbol hiperrzeczywistości i właśnie to widzimy.

Prawda jednak, którą sam widzę w tym obrazie (choć tylko fantazjuję bez należytej wprawy i kompetencji), polega jeszcze i przede wszystkim na tym, że samo to sprowadzenie, zstąpienie Boga na ziemię, czy jakkolwiek inaczej to nazywać – sama w każdym razie obecność owego Bytu nie z tego świata w ziemskiej przestrzeni – musi koniecznie oznaczać ukrzyżowanie. Właśnie dlatego, że nie istnieje żaden inny sposób by ową nadnaturalną przestrzeń – rzeczywistą mimo tej nadnaturalności – zobaczyć, przedstawić, wyrazić po ziemsku namacalnie. Inaczej niż przez ten krzyż, który widzimy. Że jedyną namacalną postacią nadziemskiej rzeczywistości – taką do zobaczenia i dotknięcia na ziemi – jest właśnie siatka krzyża i wnętrze zawieszone gdzieś wokół, gdzieś wkoło krzyża rozpięte – wciąż mimo namacalności krzyża niepojęte i nienamacalne wnętrze świata prawdziwego. Trzeba by to niepojęte zabić – a gwoździe wiszą obok, przygotowane – by móc pojąć.

Myślę więc sobie, że kto nie rozumiał dotąd znaczenia animowanego szkicu i wszystkich innych tu użytych przedstawień hiperprzestrzeni, teraz już je jednak rozumie, albo chociaż przeczuwa.

A jeszcze jest Platon i jego jaskinia – wśród mnóstwa innych cudzych dzieł i myśli wybitnych, które dałoby się tu przywołać. No, jaskinia narzuca się silnie sama z siebie. Żyjemy w niej i to co widzimy, to ledwie cienie rzeczywistości prawdziwej. Platońska figura tak się już sprała w częstym (nad)używaniu, że dziś chyba nie doceniamy ontologii, o której Platon opowiada. Bo przecież nie epistemologii ta opowieść dotyczy. Mówi nam Platon wprawdzie, że gdybyśmy doznali szczęścia widzenia światła prawdziwego – nie umielibyśmy go pojąć. Próbki właśnie doświadczyliśmy. Platon zdaje się sugerować, że kondycja więźnia jest nam przyrodzona, że na kajdany jesteśmy skazani. To niemal na pewno prawda, jak również widzieliśmy. Gdybyśmy je mogli zrzucić, początkowe niezrozumienie byłoby jednak przejściowe, choć przynosiłoby cierpienie i trwałoby długo. W końcu jednak pojęlibyśmy, że to owo zewnętrzne światło jest jedyną prawdziwą rzeczywistością – i to jest prawdziwą intencją tego fragmentu Dialogów. Ontologia i ludzka egzystencja wobec niej, a nie teoria poznawania świata w trudzie i cierpieniu.

Nadzieję być może da się pokładać nie tylko w zerwaniu kajdan i opuszczeniu jaskini. To jest przecież – i tu analogia się kończy – jedyna rzeczywistość, która nam jest dana. Platon miał oczywiście tę świadomość, dlatego prawdopodobnie sądził, że zerwanie kajdan w rzeczywistości możliwe nie jest. Jednak naturę „prawdziwego światła” da się pojąć również z cienia, a tego Platon nie podkreślał. Próbą dowodu w tej sprawie jest niniejsze. Czy się ten dowód udał, wiedzą Czytający, o ile którykolwiek dotarł aż tu. Skoro jaskini nie opuścimy nigdy inaczej jak tylko myślą – na pewno odpowiada to platońskim przeświadczeniom – to dla nas jest w zasadzie wszystko jedno, czy „prawdziwe światło” istnieje inaczej niż tylko w myślach. Czy więc np. matematyka, jej idee i konstrukcje, sama logika wreszcie, prawda i fałsz istnieją naprawdę, czy tylko w naszych myślach i jako takie są mniej realne od rzeczy, które na co dzień widzimy? Sam Platon wątpliwości w tej sprawie nie miał. „Prawdziwe światło” jest dlań bardziej realne niż konkret jaskini. Ale może „prawdziwe światło” jest właśnie myślą. Może to sama myśl, a nie światło, którego myśl dotyczy, jest właśnie prawdziwsza od kajdan. Ale Platon przy tym jeszcze przecież mówi o myślącym prawdziwie: „na pewno by go zabili”.

To chyba gorzka uwaga o śmierci Sokratesa, w którego usta Platon przecież wkłada w Dialogach własne słowa. Przedziwnie jednak wygląda w tym kontekście ten dialog, który tu uzurpacyjnie zaimprowizowałem, każąc Platonowi i Dalemu komentować się nawzajem. Czyją dokładnie śmierć Platon przewiduje? Czy zginąć ma „oświecony”, czy może np. sama „światłość”? Patrząc na obraz można różnych odpowiedzi udzielić w tej sprawie. Jest przecież w zasadzie truizmem powiedzieć, że umiera myśl kogoś, kto godzi się żyć wśród fałszywych cieni lub poza własną wolą jest na nie skazany. Jakiegoś jednak – myślę sobie – innego znaczenia nabierają takie myśli, jeśli na rzecz, wydawałoby się, dobrze znaną spojrzeć wracając z podróży w nadprzestrzeń, prawda?

* * *

W nieznośnie zaś konkretnym kontekście szkoły… Da się więc z jednej strony spytać, w jakim właściwie celu dręczymy dzieci tabliczką mnożenia. Albo z drugiej strony, odwrotnej: po co opowiadać im historie tak niestworzone, tak zawiłe i tak jawnie nie z tej ziemi?

Zadania dla nauczycieli:

1. rozumieć powyższe;
2. ocenić przydatność i jeśli ocena będzie w jakiejś części pozytywna:
3. opracować wyjściowy zestaw opowieści dla dzieci, ilustracji, odniesień kulturowych – na odpowiednim poziomie rozwoju dzieci i zgodnie z ich zainteresowaniem;
4. sformułować zestaw problemów tropem np. pytania o wyobrażenie 10 tysięcy liczb, albo (wychodząc „od środka” rozumowania) czy liczba 1111 istnieje, skoro właśnie widzimy, że istnieć nie może;
5. umiejętnie odpowiadać na pytania dzieci;
6. z wyczuciem wracać do pytań własnych;
7. nie wymagać „opanowania materiału”;
8. rozpoznać zagadnienia poznawane „przy okazji” (jak algebra w układzie kartezjańskim).

Zagadnienia do rozwinięcia i uzupełnienia dla autorów (na różnych poziomach zaawansowania adresatów – z wyjaśnieniami na jak najbardziej podstawowym poziomie):

1. krytyka i korekty -- o co proszę;
2. inne konstrukcje hiperprzestrzennych brył – np. czworościan – i ich ewentualne komputerowe „eksploratory”;
3. algebra i geometria hiperprzestrzeni, w tym np. obrót w przestrzeniach kartezjańskich;
4. wstęp do topologii;
5. teoria grafów;
6. czasoprzestrzeń, transformacje, względności, prawa zachowania, symetrie;
7. topologia kostki Rubika, model obrotów i przekształceń w kostce, współrzędne biegunowe, inaczej konstruowane przestrzenie, równoważność;
8. programowanie arytmetyki dziesiętnej w macierzach;
9. komputerowa „gra”: projekt czteroprzestrzennego labiryntu (logika przestrzeni), przemierzanego dzięki rozwiązaniu problemów logicznych, geometrycznych, probabilistycznych, algebraicznych; „udekorowanego” dziełami sztuki, literatury i filozofii.