Poniżej widzimy trójkąt Pascala. Zgodnie z założeniami niniejszego, umieszczam go tu dla nauczycieli, rodziców lub innych osób, które chcą uczyć dzieci podstaw matematyki. Nie jest dla dzieci, choć akurat trójkąt Pascala (oraz być może kilka innych tego rodzaju konstrukcji wynalezionych w historii matematyki przez innych autorów) zawiesiłbym dzieciom na ścianie jako swego rodzaju „przedmiot kontemplacji”, do którego na się co jakiś czas nazwiązywać, pokazując na nim znaczenie tkwiących w nim wzorców i symetrii. Będzie to można robić przez „całą podstawówkę” albo i dłużej. Niezupełnie od początku, bo przecież tu zaczynamy od dzieci, które jeszcze nie liczą, mogą mieć kłopot z zapisem (ten będzie przedmiotem dopiero następnej części) itd.

Konstrukcja trójkąta jest tak prosta, że właściwie na pierwszy rzut oka nie wiadomo, czemu on miałby służyć. Jeśli założyć, że na zewnątrz trójkąta leżą niewidoczne tu zera, to każda liczba w tym trójkącie będzie sumą dwóch, które są nad nią na skos: lekko na lewo i lekko na prawo, poczynając od jedynki umieszczonej na czubku. W trzecim rzędzie w środku jest 2 = 1 + 1, w czwartym rzędzie dwukrotnie występuje 3 i raz jest równe 1 + 2, a drugi raz 2 + 1. Potem z kolei 4 = 1 + 3; 6 = 3 + 3 itd. Trójkąt Pascala ma przy tej dziwnie prostej konstrukcji mnóstwo nieoczywistych „znaczeń”, a fakt, że wszystkie one „spotykają się” w tak zapisanym ciągu wygenerowanym poprzez zwykłe dodawanie elementów poprzednich jest charakterystycznym dla matematyki „zbiegiem okoliczności”.

Krótki przegląd niektórych z tych znaczeń. Liczby w kolejnych wierszach są więc np. współczynnikami rozwinięcia wyrażenia \((x+1)^n\) – przy czym \(n\) jest równe numerowi wiersza (pomijając pierwszą jedynkę, która ma numer \(0\)) – do postaci „normalnej”. Np. \((x+1)^2 = 1x^2 + 2x + 1\); \((x+1)^3 = 1x^3 + 3x^2 + 3x + 1\); \((x+1)^4 = 1x^4 + 4x^3 + 6x^2 + 4x + 1\) itd. Rozwijanie takich wyrażeń potęgowych przybiera w szkole postać słynnych wzorów skróconego mnożenia. Dzieci niemal zawsze wkuwają je na pamięć. Niektóre z tych wzorów poznamy z dziećmi tutaj – i dzieci je po prostu zobaczą, widząc, skąd się bierze nawet nie wzór (nie będziemy z dziećmi pisać, chyba, że bardzo chcemy), a raczej sama opisywana nim zależność. Sumy liczb w kolejnych wierszach są odpowiednimi potęgami \(2\) (znów wierzchołek ma numer \(0\)). Kolejne liczby są wartościami odpowiednich tzw. dwumianów Newtona, określających różne rzeczy, np. ilość możliwych \(k\)-elementowych podzbiorów \(n\)-elementowego zbioru (\(n\) jest numerem wiersza, a \(k\) – kolejną pozycją w wierszu). Zadaniem niezależnym od tego rodzaju związków, a trudnym i być może ciekawym dla już „wkręconych” w tropienie regularności i ich wyjaśnianie dzieci jest też np. umieć wskazać wartość \(k\)-tej liczby \(n\)-tego wiersza trójkąta bez mozolnego wypisywania wszystkich liczb poprzednich. No, zajęć z trójkątem jest mnóstwo i same w sobie starczyłyby może nawet na całą szkołę.Nas interesują tu bezpośrednio zaznaczone kolorami „przekątne” trójkąta. Pierwsza z nich zawiera kolejne liczby naturalne, druga – liczby zwane trójkątnymi, trzecia – liczby czworościenne, a czwarta – liczby dające się ułożyć w czworościan w przestrzeni czterowymiarowej. Nie jest to przypadek – czworościan, czyli bryła, której ściany są trójkątami, da się widzieć jako „uogólnienie” trójkąta z dwóch wymiarów do trzech. Dziwny czworościan czterowymiarowy (w rzeczywistości ma więcej ścian, niektóre same są czworościanami, a niektóre trójkątami) jest podobnym uogólnieniem w górę. W kolejnych przekątnych mamy liczby odpowiadające bryłom skonstruowanym w przestrzeniach o coraz większej ilości wymiarów. Nadprzestrzenie są ostatnim z tematów proponowanych w tym dziale, ale tu je zostawmy. Tu chcę zaproponować przede wszystkim kilka zabaw z klockami, które pokażą dzieciom pewne nieoczywiste związki liczb.

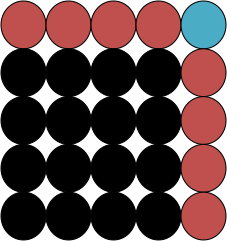
Jak to zostało zaznaczone we wstępie niniejszego cyklu, omawiany tu materiał powinien następować raczej po pierwszych „wprawkach” w myśleniu geometrycznym i potem geometria powinna być przez dzieci studiowana (to słowo chcę podkreślić i dosłowność jego znaczenia także) równolegle z omawianymi tu zagadnieniami, bo one okazują się na wiele sposobów wspólne, a na wiele – unikalne. Bo liczby naturalne wcale nie są naturalne prawdziwie – również nie w ten sposób, żeby były łatwiej zrozumiałe dla dzieci. Dzieci powinny już raczej mieć intuicje o tym, że liczba określa np. długość i odległość, a nie tylko ilość. Ćwiczenia w liczeniu np. kasztanów, ale też i takie obserwacje, jak tu niżej proponowane, mają w stosunku do myślenia geometrycznego między innymi wadę ujawniającą się np. tym, że o ile np. 10 – 7 = 3, to klocków od 7. do 10. jest niestety 4 (w których to okolicznościach dorośli czują się często zmuszeni liczyć na palcach, nie potrafiąc posłużyć się uogólnieniem, że ilość od M do N jest zawsze M – N + 1). Nie wchodząc tu już w szczegóły, dzieci powinny mniej więcej równocześnie odkrywać np. w jaki sposób na rysunku obok liczba na osi C jest sumą liczb zaznaczonych na osiach A i B (przeciągnięcie czerwonych kropek w odpowiednie miejsca uruchomi kalkulację). Równoczesność i wielowątkowość takiego studiowania jest oczywiście wartością samą w sobie – tu chciałbym zwrócić przy okazji uwagę na jeden z wielu aspektów roli nauczyciela. Otóż rysunek obok pochodzi z niewielkiego komputerowego programu (do załadowania kod Flash), który dzieci potrafiące to robić albo stawiające właśnie pierwsze kroki (samo w sobie zajęcie jest kształcące oczywiście nie tylko w informatyce) mogą zrobić dla tych, które tego nie potrafią, na podstawie projektu opracowanego przez dzieci rozumiejące lub właśnie poznające talesowskie proporcje i pojęcie średniej – po to, żeby te pojęcia zademonstrować dzieciom, które się z tym jeszcze nie zetknęły. Programik to geometryczny kalkulator do dodawania. Jedną więc z ról nauczyciela jest aranżować tego rodzaju współpracę w powstających ad hoc grupach dzieci różniących się wiekiem, zainteresowaniami i poziomem umiejętności (ktoś umiejący rysować mógłby np. zadbać o atrakcyjny wygląd rysunków, szkiców, programów komputerowych itd.)

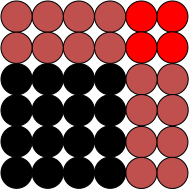
Czym są liczby trójkątne? To liczby kropek, klocków, kulek potrzebnych do zbudowania odpowiedniej liczby „pięter” trójkąta jak ten na rysunku. Może to być jedna z pierwszych dziecięcych wprawek w liczeniu, w którym nie chodzi o odpowiedź na pytanie typu „ile kasztanów w koszyku ma Marysia?”, ale o strukturę, prawidłowości i wzorce. Ważne jest, by dzieci raczej w tego rodzaju sytuacjach wykonywały swoje pierwsze dodawania. Oczywiście ważne to jest wyłącznie wtedy, kiedy celem jest może nie aż nauka matematyki, ale po prostu kontakt z myśleniem typowym dla matematyki.

„Jednopiętrowa” liczba trójkątna, to 1; „dwupiętrowa” – 3; „trzypiętrowa” – 6; „czteropiętrowa” – 10 itd. Może nie trzeba pokazywać ich dzieciom na trójkącie Pascala, ale można, bo trójkąt zawiera pewną odpowiedź na pytanie „dlaczego”. Ważne jest pokazać, że na kolejnych „piętrach” leżą kolejne, rosnące o 1 liczby kulek i liczba kulek w piętrze odpowiada numerowi piętra. Liczba i numer, to dwa pojęcia, które nie muszą oznaczać tego samego i warto dzieciom zwrócić na to uwagę (przy okazji być może wyjaśniając także językowe rodzaje liczebników). Mamy więc pierwszą, drugą, trzecią, czwartą liczbę trójkątną. Oraz oczywiście dalsze. Zależności rządzące liczbami trójkątnymi są tak oczywiste, że niemal nie wymagają obserwacji. Jest więc np. jasne, że N-ta liczba trójkątna jest sumą 1 + 2 + … + N. Przyda się jednak dzieciom podkreślić, że do zbudowania trójkąta (N + 1) potrzeba trójkąta N i jeszcze N + 1 kulek. Widać to na trójkącie Pascala w sposób bezpośrednio wynikający z jego konstrukcji – odpowiedni element zielonej przekątnej jest sumą poprzedniego elementu zielonego i poprzedniego szarego. To rodzaj bardzo elementarnego rozumowania indukcyjnego – te same zależności ukażą się nam jeszcze tyle razy, ile będziemy tylko chcieli, a dotyczyć będą rzeczy już zupełnie nieoczywistych.

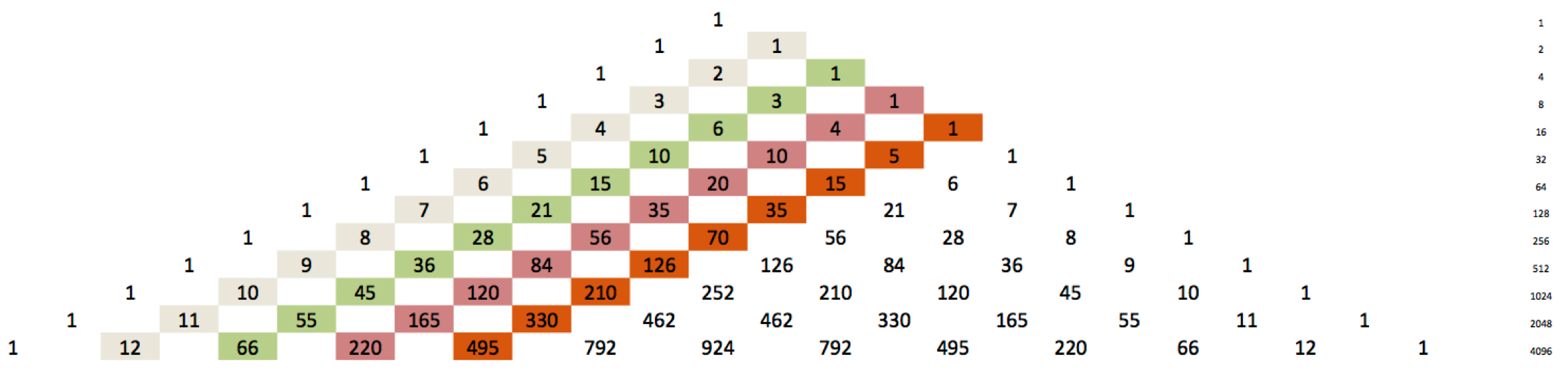
Liczby czworościenne to konstrukcja przestrzenna. Należy z klocków bądź kulek zbudować opartą na trójkątnym wzorcu piramidkę. Zadanie jest identyczne – ocena liczby klocków potrzebnych do zbudowania piramidy o liczbie pięter N. To jest kolejna, różowa przekątna trójkąta Pascala. Każde piętro piramidki ma tyle kulek ile ich jest w odpowiednim trójkącie. Zatem do zbudowania czteropiętrowej piramidki należy wziąć trzypiętrową piramidkę i dodać czteropiętrową liczbę trójkątną, co znów odpowiada wprost konstrukcji trójkąta Pascala.

Jak wspomniałem, kolejna, czerwona przekątna w trójkącie Pascala, zawiera podobnie określone liczby, które tym razem umieszczono w czworościanie umieszczonym w hiperprzestrzeni. Uzyskuje się tę bryłę umieszczając w przestrzeni kolejny wierzchołek i wznosząc go tym razem wzdłuż osi czwartego wymiaru przy zachowaniu równoboczności odpowiednich trójkątów. To kolejny duży i świetny temat, który dobrze byłoby pociągnąć z dziećmi – nie na wstępnym etapie pierwszych zabaw w świecie klocków, ale raczej w ramach nauczania początkowego. Nie został tu jeszcze opracowany – studium hiperprzestrzeni jest tu ograniczone do analizy sześcianu, co ma związek ze strukturą systemu dziesiętnego i samym kształtem wielowymiarowych przestrzeni kartezjańskich. Tu natomiast „hiperprzestrzenna wyobraźnia dziecka” uzyskałaby kolejne wsparcie, bo ta sama indukcyjna prawidłowość trójkąta Pascala nadal tu obowiązuje, dając kolejną, nową podpowiedź właściwego rozumienia przestrzeni: czworościan czterowymiarowy (o pięciu czworościennych ścianach) będzie miał tyle klocków ile ich miał poprzedni taki czworościan i odpowiedni czworościan trójwymiarowy. Objętość sześcianu w hiperprzestrzeni przyrasta w inny sposób, nie dając podpowiedzi wyobraźni.

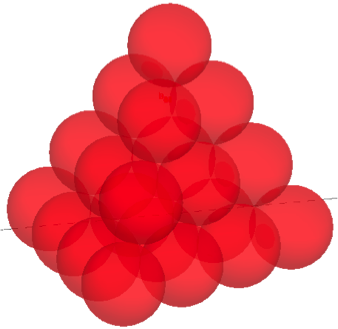
Liczb kwadratowych, sześciennych i następnych nie ma wśród wierszy i przekątnych trójkąta Pascala wprost, choć są w tym trójkącie współczynniki wielomianów opisujących arytmetykę w odpowiednich zbiorach. Ale związki istnieją i warto je z dziećmi prześledzić. Liczba klocków potrzebnych do ułożenia ściany o wysokości (boku) \(N\), to oczywiście \(N^2\). Jeżeli chcemy wysokości 1, potrzebny jest 1 klocek, jeśli 2 – potrzebne są 4, jeśli 3 – 9, 4 – 16 itd. To banał, ale – podkreślmy znowu – nie o to chodzi, by dzieci sprawnie liczyły, ani o to, by mnożyły, czy po prostu dodawały. Chodzi raczej o to, by zauważyły zaznaczoną na rysunku sytuację. Jeśli mamy już ścianę o jakiejś wysokości \(N\), to dołożenie kolejnego piętra tak, żeby ściana pozostała kwadratem, musi oznaczać jej poszerzenie – w efekcie zawsze dodajemy \(2N+1\) klocków, jak zaznaczono na rysunku. Liczba dodawanych klocków jest zawsze nieparzysta, ale wynika stąd „wzór skróconego mnożenia”: $$(N + 1)^2 = N^2 + 2N + 1.$$Tego wzoru nie da się przecież nawet zapisać dzieciom – wystarczy razem z nimi odkryć, że dokładamy zawsze \(2N + 1\). Ale kolejnym takim spostrzeżeniem jest, że ściana o wysokości np. 5 jest zawsze sumą 5 kolejnych liczb nieparzystych: \(1 + 3 + 5 + 7 + 9\), a o tym wie mało który dorosły. Maluchy są to w stanie zauważyć i zrozumieć (bo to po prostu widać). Asystującym przy tym ewentualnym odkryciu dorosłym warto zwrócić uwagę na towarzyszącą temu odkryciu logikę, bo to jest znów wspomniana indukcja matematyczna. Fakt, że $$N^2 = 1 + 3 +…+ 2N-1$$ (a sładników tej sumy jest dokładnie N) oraz wzór skróconego mnożenia $$(N + 1)^2 = N^2 + 2N + 1$$ wynikają z tej zasady. Pierwsze jest prostą konsekwencją spostrzeżenia, że zawsze dodajemy \(2N + 1\), a drugie jest innym sformułowaniem tej samej zasady – jeśli wiemy, ile to \(N^2\), to wiemy również, ile to będzie \((N + 1)^2\) – po prostu o \(2N + 1\) więcej. Indukcję możemy próbować uświadomić dzieciom. Można się teraz bawić tymi liczbami, szukając np. związków miedzy liczbami trójkątnymi i kwadratowymi. Wypiszmy je sobie:

Da się zauważyć bez specjalnego trudu, że poczynając od drugiej z kolei każda liczba kwadratowa składa się z dwóch liczb trójkątnych. N-ta liczba kwadratowa jest mianowicie sumą N-tej i poprzedniej liczby trójkątnej. I tak: \(4 = 3 + 1\); \(9 = 6 + 3\); \(16 = 10 + 6\) itd. Co innego zauważyć, a co innego dowieść, że tak być musi. Kiedy się już wie, że każda liczba kwadratowa jest sumą kolejnych liczb nieparzystych aż do \(2n-1\), a każda liczba trójkątna jest sumą liczb do n, dowód stanie się prostym przekształceniem odpowiednich „wyrażeń algebraicznych”, co mogą zrobić starsze dzieci. Ale rzecz właśnie w tym, że tego robić nie trzeba, bo wystarczy narysować, jak obok. I zauważyć, że dowód jest gotowy. Każdy tak narysowany kwadrat będzie się musiał składać z dwóch trójkątów różniących się dokładnie o jedno piętro w poszukiwany przez nas sposób. To jest dowód, który da się zaproponować dzieciom u progu „nauki szkolnej”, nie umiejącym w zasadzie liczyć, a przypominam, że zarówno szkoła oficjalna, jak i ogromna większość jej reformatorów, włącznie z radykałami spoza systemu – wszyscy dawno już pozbyli się dowodzenia i myślenia abstrakcją z treści tego, czego się dzieci uczą.

Przywołany we wstępie Platon da się tu zacytować dorosłym, którzy uczą dzieci. Jak pamiętamy, skuci kajdanami więźniowie w platońskiej jaskini widzieć mieli wyłącznie cienie rzeczy prawdziwych. Cienie są uboższym i przez to zafałszowanym obrazem rzeczywistości. A jednak więźniowie w opisie Platona opanowują całą sztukę widzenia tej zniekształconej rzeczywistości, uczą się przewidywać i nawet w jakiś sposób wyjaśniać zjawiska obserwowane w tej postaci, nie zdając sobie nawet sprawy z fałszu przedstawień i nie próbując dociec ukrytej prawdy. Pokazane tu problemiki i zabawy z klockami, żetonami, czy czymkolwiek są wszystkie zbędne – szkoła już dawno nauczyła się skutecznie ćwiczyć dzieci w rachowaniu bez tego rodzaju myślenia. To rachowanie – jak się tu jeszcze wielokrotnie okaże – bardzo przypomina szkołę interpretacji cieni rozwiniętą przez platońskich więźniów. Chodzi o to, by próbować widzieć głębszą, rzeczywistą strukturę rzeczy, o których opowiadamy, choćby to były tylko liczby u progu szkoły podstawowej.

Wspomnianego przekształcenia „wyrażeń algebraicznych” pokazującego związek liczb kwadratowych z trójkątnymi nie trzeba więc – i wcale nie warto – zostawiać dzieciom starszym. Klockami da się manipulować dalej i odpowiednie trójkąty złożyć również w kolejny tu pokazany sposób. No, informacji jest w tym rysunku więcej i wszystkie się nam przydadzą – zanim nauczymy się liczyć. Widać więc, że i może nawet dlaczego suma dwóch kolejnych liczb (jedna o jeden większa od drugiej) jest zawsze nieparzysta. Można spróbować w ten sposób budować w umysłach dzieci intuicję abstrakcyjnego pojęcia

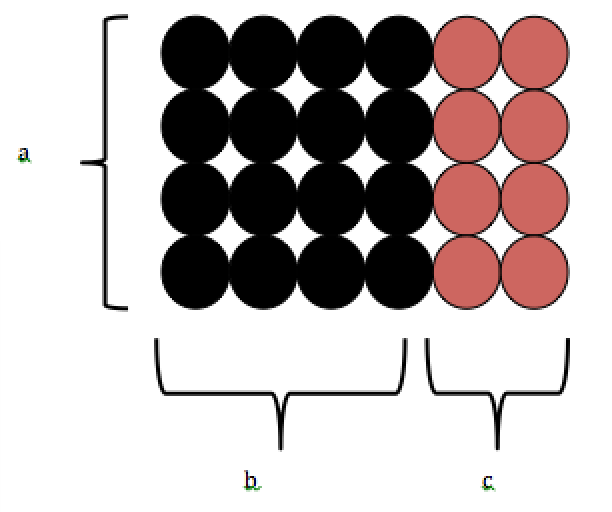
Wspomniana wcześniej różnica między ilością, a długością lub odległością, utrudnia tu znacznie odnalezienie związków pomiędzy powyższym, a zależnością pomiędzy polem trójkąta i prostokąta. Niemniej w niektórych przypadkach warto spróbować, bo proszę tylko spojrzeć, ile intuicji da się zaproponować dzieciom. O ile wiedzą, co mniej więcej znaczy mnożyć (a to oczywiście warto pokazywać właśnie przy tych okazjach związanych z klockami), warto się postarać o to, by mnożeniu towarzyszyła taka quasi-geometryczna intuicja, która pozwala ocenić ilość kropek tego prostokąta na \(5 \cdot 6 = 30\). Kropek czerwonych i czarnych jest tyle samo, więc po \(15\). No, niestety niezupełnie to jest ten sam pamiętany ze szkoły wzór na pole trójkąta, bo nie jest to \(\frac {ah}{2}\)… Przekładając to na trójkąt, należałoby pokazać dzieciom, że musielibyśmy w tym przypadku dzielić kropki na pół i że pole, długość i miary geometryczne, różnią się w ten sposób od liczebności. Niemniej zależność jest podobna – zamiast \(a\) jako podstawy, należy skorzystać z \((a + 1)\). W ten sposób prostokąt podzielony na pół daje cały trójkąt. Prostokąt ma zaś podstawę powiększoną o \(1\). Dostajemy w ten sposób wynalazek małego Gaussa na sumę szeregu arytmetycznego.

Czy to nie jest przesada, przy samych początkach liczenia? Skąd np. dzieci miałyby „znać wzór” na pole trójkąta? No, nie wzór, uchowaj Boże! Zakładamy w tym miejscu jedynie, że „naukę liczenia” rzeczywiście poprzedzają „wprawki” w myśleniu geometrycznym. W tym taka – jeden przykład z tego nieopracowanego tu jeszcze działu – w której dzieci próbują odgadnąć, czego jest więcej na pokazanym im rysunku: zielonego, czy czerwonego. Odpowiedzi udziela dorysowanie pionowej przerywanej linii \(h\), której pokazywany dzieciom rysunek nie zawiera, oraz obserwacja, że kolory dzielą teraz na połowy dwa prostokąty. Jeśli wiemy (z liczenia guzików), że pole prostokąta to \(ah\), to pole trójkąta jest o połowę mniejsze. Formuła Gaussa na sumę szeregu posługuje się pojęciem średniej, które da się zastosować również do trójkąta. Gdybyśmy mianowicie narysowali poziomą linię równoległą do podstawy i przesuwali nią w górę i w dół (proszę spróbować), jej długość zmieniałaby się od \(0\) do \(a\), przyjmując średnią wartość \(\frac a2\). Pole trójkąta jest więc polem prostokąta uzyskanego ze średniej długości podstawy. Podobne intuicje pozwalały Archimedesowi porównywać pola różniących się między sobą figur i objętości brył – staną się potem podstawą w zagadnieniach rachunku różniczkowego i całkowego.

Oczywiście związki z polami figur, formuła Gaussa itd. są problemami stosunkowo trudnymi i trzeba by dla nich znaleźć stosowny moment oraz okazję – na pewno musiałoby się to stać po szeregu obserwacji prostszych i bardziej podstawowych, jak poniższe.

Widać tu zarówno, że \(6 \cdot 4 = 4 \cdot 6\), jak to, że iloczyn tych liczb jest ilością „jabłek w skrzynce”, czyli polem „powierzchni” oraz oczywiście, że \(4 \cdot 6 = 6 + 6 + 6\) + 6. To jest najzupełniej banalne, ale dzieci nie bardzo już wiedzą, że np.: \(a(b + c) = ab + ac\). To zaś jest nie tylko zrozumiałe, ale po prostu widoczne na rysunku. W czarnym prostokącie jest \(ab\) kropek, w czerwonym – \(ac\). W połączonym prostokącie jest \(a(b + c)\), bo taką „długość” ma dłuższy z jego boków, a oczywiście ilość wszystkich kropek jest równocześnie równa sumie ilości w poszczególnych prostokątach „składowych”. Na kolejnym szkicu widać „wzór skróconego mnożenia”, który w zasadzie pozostaje poza możliwością pojmowania w szkole podstawowej i który uchodzi za osiągnięcie uzdolnionych matematycznie gimnazjalistów (którzy nieodmiennie ów wzór opanowują pamięciowo z wykorzystaniem wielu dziesiątek zadań „na stosowanie” tego wzoru). Tu po prostu wystarczy się przyjrzeć, by dostrzec, że i dlaczego \((a+b)^2 = a^2 + 2ab + b^2\). To samo da się zrobić dla trzeciej potęgi. Warto pokazać dzieciom przypadek sześcianu jako uogólnienie kwadratu. Zarówno algebraicznie, jak geometrycznie. I może nawet da się spróbować zrobić to dla kolejnych, choć do tego potrzebny byłby już specjalny rodzaj „widzenia”.

Kolejne „zastosowanie” liczb naturalnych, od których nie chcielibyśmy zaczynać „nauki liczenia”, a które może sprzyjać rozwijaniu „zmysłu obserwacji”, analizy i wnioskowania – kombinatoryka i prawdopodobieństwo dla maluchów. Gry i zabawy z użyciem kostek (zawsze lepiej, gdy mają różne ilości ścian i nie są zawsze tylko sześcianami) dają tu znakomite okazje. Tu tylko jeden przykład zasad gry, której „fabułę” można określić dowolnie. Gry z większą ilością kostek są zresztą zawsze lepsze – nie tylko i nie przede wszystkim dlatego, że wymuszają dodawanie, mogą wymuszać również mnożenie oraz – przy pewnej determinacji nauczyciela – również dzielenie. Chodzi głównie o obserwację „przestrzeni zdarzeń” losowych. Tu przestrzeń tę widać w jej „dosłownie abstrakcyjnej postaci”.

Mamy więc dwie sześcienne kostki do gry, prostą planszę i zestaw pionków – powiedzmy po trzy dla każdego dziecka. Dzielimy dzieci – bardzo to lubimy robić w szkole – na trzyosobowe grupy. Plansze zawierają pola oznaczone numerami lub – jeśli trzeba, kiedy dzieci nie radzą sobie z cyferkami – kropkami od 1 do 12. Każde dziecko ustawia na planszy po trzy swoje pionki (dzieci stawiają je w losowo ustalonej kolejności na przemian, przy czym ustalamy, czy na jednym polu wolno ustawiać więcej niż jeden pionek, a jeśli więcej – to czy tylko pionki jednego gracza, czy panuje tu zupełna dowolność). Rzucamy kostkami, liczymy sumę oczek i jeśli mamy na odpowiednim polu swój pionek (albo pionki), zdejmujemy go (je) z planszy. Wygrywa ten, kto pierwszy zdejmie swoje pionki. To zresztą może być nie cała gra, a tylko jej początek – chodzić może o „start z biegu” stosowany np. w regatach żaglowych.

Dzieci grają w grupach i kiedy rozstawią swoje pionki, nauczyciel zapisuje ustawienia. Kiedy wszystkie skończą grać, zapisujemy, kto w której grupie zajął pierwsze, kto drugie, a kto ostatnie miejsce. I oczywiście analizujemy te wyniki, zadbawszy o to, żeby grup i wyników było jak najwięcej i żebyśmy mieli co analizować. Chodzi o to, żeby dzieci odkryły najpierw, że pole oznaczone jedynką skazuje na porażkę, ponieważ jedynka nie wypadnie nigdy. Potem dzieci powinny zauważyć, że niektóre pole wygrywają częściej niż inne. Wyjaśnieniem, dlaczego tak się dzieje, jest właśnie „przestrzeń zdarzeń”:

Poza kombinatorycznym sensem tej tabelki, chodzi również o sens arytmetyczny. Z tego powodu zresztą warto tę grę (lub podobnie skonstruowane) wykonywać dla kostek innych niż sześcienne. Oczywiście warto również zamieniać dodawanie na mnożenie. Tu chodzi wszakże o tabliczkę dodawania i dostrzeżenie jej symetrii. Warto więc, by dzieci wpadły na to, by ją wyrysować same. Zauważą wówczas, że nie pisząc wierszami lub kolumnami, nie muszą niczego dodawać, a tylko wpisywać odpowiednie serie, co jest świetnym wstępem do następnych części materiału.

Oczywiście w związku z samą grą chodzi tu o to, że np. 2 i 12 występują w tej tabeli raz, a 7 – sześć razy. I w związku z tym siódemka wygrywa najczęściej. Da się oczywiście rzucać trzema kostkami i spróbować tę sytuację wyrysować z dziećmi, co jest technicznie trudniejsze.

Jeśli zaś wymyślimy „fabułę” odpowiednio ekscytującą, może da się dzieci zwieść i na takie manowce, że zechcą użyć czterech kostek i w podobny sposób zorientować się, który numer okaże się wygrywającym. Kombinatoryka nie występuje w żadnej tutejszej sytuacji w sposób „czysty”. Istnieją różne pary liczb dające te same sumy – to chcemy, żeby dzieci zauważyły. Natomiast obserwacja symetrii ilości wystąpień wyników w przestrzeni dwu i trójwymiarowej, o czwartym wymiarze nie wspominając, wymaga już analitycznej przenikliwości na poziomie niemal mistrzowskim – czego również spróbować byłoby warto. Dlaczego wśród 64 możliwych wyników rzutów czterema czworościennymi kostkami czwórka i dwunastka pojawią się raz – jest zrozumiałe. Dlaczego piątka i jedenastka pojawią się po trzy razy – no, to wymaga wyobraźni. Zarówno z kombinatorycznego, jak i geometrycznego punktu widzenia.

Również zanim zaczniemy dodawać, zapisując te operacje liczbami w systemie dziesiętnym (lub innym) warto pokazać dzieciom czym są sumy i wielokrotności w różnych układach. Jeśli mamy za sobą wprawki geometryczne, ten problem powinien być wyczerpany w sensie proporcji, być może też powierzchni i wszelkich miar długości. Jednak sumy, ilości i wielokrotności warto pokazać dzieciom na planszach. To m.in. jest przedmiotem następnej części materiału, niemniej tu warto pokazać dzieciom „kontemplacyjną zabawkę” w klasycznej greckiej matematyce znaną jako sito Erastotenesa.