Powinniśmy przede wszystkim „zdelegalizować” wszelkie „karty pracy” w rodzaju kwiatuszków, które na płatkach mają dodawania dające wynik widoczny w środku. Powinniśmy tego rodzaju zadania oraz zwłaszcza gry i zabawy wymagające „poważniejszych” obliczeń rozwiązywać z dziećmi przy pomocy np. opisanych niżej pomocy, pokazujących strukturę i sens tego, co się robi z liczbami, a nie jedynie ułatwiających zapamiętanie. Jest oczywiście ważne, żeby niezanadto „bolało” i żeby znaleźć dla dzieci w tych ćwiczeniach coś angażującego, przyjemnego i od czasu do czasu pozwalającego odwrócić ich uwagę od samego tylko liczenia, jednak atrakcyjność tego rodzaju nie wystarcza – powinniśmy walczyć z pamięciowym wyłącznie „opanowywaniem liczenia” i koncentrować się stale na strukturze problemu. Oraz zwłaszcza na tym, żeby przed dziećmi stawiać właśnie problemy.

Zapałki i patyczki bywają w szkole eksploatowane na różne sposoby, a wśród nich również np. na taki, który jest potencjalnie ciekawy:

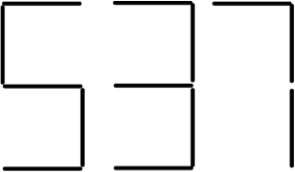
Na stole leżą zapałki ułożone w cyfrowy zapis liczby , jak obok. Trzeba teraz przestawić jedną zapałkę tak, żeby otrzymana liczba była największą z możliwych. To prosty przykład i wielu możliwości tu nie ma. Chodzi tu o to, że tego rodzaju zagadki mogą mieć jakiś cel, albo mogą być sensu pozbawione. Z cyfry do cyfry da się przestawić jedną zapałkę tak, by „zapis” pozostał sensowny i może to być tylko pozioma zapałka z cyfry 7. Oprócz tego w cyfrze 5 można przestawić zapałkę tak, by ją przerobić na 3, co nie ma sensu, skoro chodzi nam o zwiększenie liczby. Możemy postąpić odwrotnie z cyfrą 3. Zapałkę z siódemki możemy też położyć na trójce, przerabiając ją na dziewiątkę, albo na piątce, przerabiając ją na szóstkę lub dziewiątkę. Ten wybór jest dla nas ciekawy. Oczywiście rozwiązaniem jest 931. Ale chodzi o pokazanie maluchom logiki zapisu dziesiętnego. Każda cyfra ma tu oczywiście swoją rolę zależną od miejsca, na którym występuje i jeśli w tej zagadce o coś chodzi, to właśnie o to. Rzecz w tym, że opłaca się zwiększyć liczbę setek, nawet jeśli zmniejszamy liczbę w tym przypadku jedności. Oczywiście bardziej się opłaca zwiększenie liczby setek niż dziesiątek.

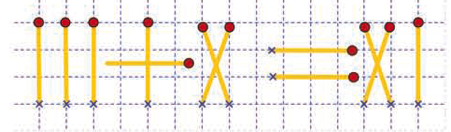
Obok widzimy natomiast przykład bezsensowny. Należy jak najmniejszą ilością ruchów doprowadzić do zapisu, który jest prawdziwy. Zadanie to spełnia wymaganie podstawy każące dzieciom przyswoić rzymski system zapisu liczb. Rzymianie jednak nie znali znaku równości i dodawania, co należy zauważyć z zażenowaniem. Być może zadanie da się wykorzystać, by z dziećmi porozmawiać o prawdzie i fałszu matematycznych oraz innych zdań, ale nie wydaje się, by przestawianie zapałek było dobrą strategią akurat w tym przedmiocie. Zapałki mają rzecz uatrakcyjnić i upodobnić do zabawy. Niewątpliwie słusznie, ale poza tym zadanie jest po prostu bezmyślne i nie uczy niczego poza być może spostrzegawczością i niezbyt odkrywczym myśleniem zdroworozsądkowym.

Generalnie umiejętność liczenia jest narzędziową sprawnością. To coś w rodzaju języka (dobrze by było, żeby był podobny do języka ojczystego, a nie drugiego – wyuczonego) i tu najgorszym, a nie najlepszym pomysłem jest uczyć się go na specjalnych lekcjach. Lepiej to wychodzi „mimochodem” w trakcie rozmów o czymś innym niż sam język przecież. Dzieci uczą się mówić, nie robiąc tego celowo. Z liczbami rzecz jest nieco bardziej skomplikowana, ponieważ liczby mają swoją strukturę i byłoby dobrze, żeby rozmaite okazje pozwalały dzieciom ją rozpoznać, a nie jedynie przyswoić nieświadomie.

Jeśli dzieci znają cyfry i uczymy je teraz zapisu liczbowego i dodawania w zakresie przekraczającym 10, to koniecznie powinniśmy dawać im okazje do zobaczenia struktury zwłaszcza zapisu dziesiętnego. Tabelkę, jak ta wyżej powinniśmy dzieciom pokazywać częściej niż oś liczbową, służącą do porządkowania liczb i budowania intuicji typu: jeśli \(a>b\), to \(b<a\); jeśli \(a>b\) i \(b>c\), to \(a>c\) (co zresztą dzieci dostrzegą również na tabelce). Zakładamy tu – raz jeszcze przypomnę – że „przerobiliśmy” z dziećmi geometrię i że dzieci wiedzą w związku z tym, co to jest długość, odległość, powierzchnia. Powinny również oczywiście wiedzieć o istnieniu uporządkowanej osi liczb (i również o tym, że poza wartościami całkowitymi istnieje na niej nieskończoność innych wartości). Warto używać takich tabliczek i kolorować na nich kolejne wielokrotności dwójki, trójki itd. Niektóre układy (proszę sprawdzić) wyglądają ciekawie.

Kolejne wielokrotności 9 leżą na przekątnej: 9, 18, 27 itd. (mają jeszcze kilka innych ciekawych własności, ale o tym osobno); kolejne wielokrotności 8 – na przekątnej nieco bardziej pochyłej, utworzonej ruchami konika szachowego: 8, 16, 24, 32, 40, po czym wracamy do prawej krawędzi i znowu: 48, 56 itd. O tych rzeczach będzie mowa w kolejnym materiale.

Jedną z ogromnych zalet tej tabliczki jest to, że stanowi ona kalkulator do dodawania, użyteczny zwłaszcza w kombinowaniu „przejść przez 10”. I tak: do czegokolwiek dodajemy 9, możemy odliczać 9 pól w prawą stronę, przechodząc do kolejnego wiersza, jeśli trzeba (a na ogół trzeba), ale też możemy pójść do następnego wiersza i cofnąć się w lewo o jedno pole. Operacja z przechodzeniem do następnego wiersza i cofaniem się o jedno pole okaże się nieopłacalna zaledwie w przypadku dodawania 9 do okrągłych liczb w rodzaju 40. Z wielokrotnościami 8 jest podobnie (choć nie aż tak prosto). Itd.

Wprawa w dodawaniu na tej tablicy oraz w odczytywaniu liczb na pokratkowanej planszy bez oznaczeń liczbowych, spowoduje również poruszanie się w jej obrębie na poziomie tabliczki mnożenia, zwłaszcza u wzrokowców. Umieszczona tu prosta gra zawiera dwa poziomy trudności w identyfikacji liczb na planszy z polami o nieoznaczonych wartościach. Należy pomóc odnaleźć kości psu. Pies podaje numer, który trzeba wskazać myszą. W wersji łatwiejszej nagłówki kolumn i cyfr są oznaczone numerami, w wersji trudniejszej tych oznaczeń nie ma.

Plik .swf (obsługiwany przez przeglądarkę dokumentów Flash) do pobrania tu.

Plik .fla z kodem źródłowym do pobrania tu.

Identyczny układ w kolejnej zabawie służy do odejmowania i dodawania. Tym razem używając strzałek klawiatury należy przenosić małego białego pieska widocznego na planszy, wykonując działania podawane przez większego z psów.

Poza innymi zaletami tej tabliczki i zwłaszcza jej wersji komputerowej, to jest niezły trening w przekraczaniu progu 10. Dziecko w naturalny sposób buduje sobie strategie, ustalając np. , kiedy wykonując odejmowanie -48 warto najpierw odjąć 50, a potem dodać 2. Sytuacje łatwiejsze w obliczeniach pamięciowych stają się trudniejsze na planszy i odwrotnie.

Plik .swf.

Plik .fla z kodem źródłowym.

Inną metodą na osiągnięcie podobnego rodzaju rozumienia, która w związku z tym powinna być stosowana równolegle, jest system jednakowych żetonów (odpowiadających jednościom) pakowanych następnie w woreczki dziesiętne, te z kolei po dziesięć w woreczki setne, tysięczne… – może tyle starczy. Woreczkami warto się posługiwać zwłaszcza wtedy, kiedy przyjdzie do algorytmów pisemnego dodawania, odejmowania i dzielenia. „Odejmij 11” będzie w tej sytuacji oznaczało zabrać dziesiętny woreczek (być może rozpakowując i usuwając woreczek setny – pożyczanie z setek w odejmowaniu pisemnym) i jeden żeton pojedynczy. „Odejmij 19” może znaczyć (podobnie jak na planszy) zabranie dwóch woreczków dziesiętnych i zwrócenie (dołożenie) jednego żetonu pojedynczego. Itd. Mnożenie będzie się odbywało osobno dla żetonów i woreczków każdego rodzaju, a zwrócić trzeba będzie uwagę na logikę porządkowania wyniku tak, by żetony były popakowane zgodnie z ustaloną, wyjaśnioną i znaną dzieciom zasadą. Ta zasada powinna być dzieciom znana i przez nie zrozumiała na operacyjnym poziomie zanim odpowiednie działania zaczną być zapisywane i wykonywane na papierze. Woreczki jako model poznawczy przydają się również niestety sporo starszym dzieciom, bo one nie rozumieją, dlaczego algorytmy działań skonstruowane są tak, a nie inaczej. Woreczki są nader użytecznym narzędziem. Aczkolwiek nieco zawstydzające dla starszych dzieci – bo kojarzące się z aktywnościami przedszkolaków – da się je zaproponować dzieciom przy okazji eksploracji systemów innych niż dziesiętne.

Sam zapis można pokazać kolejną metodą stosowaną w Montessori – przy pomocy nieco innego rodzaju tabliczek, które ułożone jedna na drugiej pozwalają ułożyć dowolną liczbę.