„Przede wszystkim czy myślisz, że tacy ludzie mogliby z siebie samych i z siebie nawzajem widzieć cokolwiek innego oprócz cieni, które ogień rzuca na przeciwległą ścianę jaskini?”

Tak retorycznie pytał Sokrates w dialogu, w którym Platon umieścił swego brata, Glaukona, w charakterze rozmówcy mistrza. Znamy platońską alegorię jaskini, więc znamy również to dręczące ludzi od dawna podejrzenie, że rzeczy nie są w istocie takie, jakimi je widzimy.

Sześcioletnia Marysia Wicher odkryła taką oto przedziwną prawidłowość na liście kolejnych iloczynów szóstki:

\(6 \cdot 1 = 6\)

\(6 \cdot 2 = 12\) (mnożymy przez 2 i na końcu wyniku jest 2)

\(6 \cdot 3 = 18\)

\(6 \cdot 4 = 24\) (mnożymy przez 4 i na końcu wyniku jest 4)

\(6 \cdot 5 = 30\)

\(6 \cdot 6 = 36\) (mnożymy przez 6 i na końcu wyniku jest 6)

\(6 \cdot 7 = 42\)

\(6 \cdot 8 = 48\) (mnożymy przez 8 i na końcu wyniku jest 48)

itd.

Zagadkowy "zbieg okoliczności" przy parzystych mnożnikach szóstki jest ozywiście prawidłowością ogólną i rzecz jasna przy większych mnożnikach, np. 32 również 2 będzie liczbą jedności wyniku. Warto przyjrzeć się także liście nieparzystych mnożników i dostrzec prawidłowość -- liczby jedności wyników mnożenia rosną o 2: 6, 8, 10, 12, 14 itd. W rzeczywistości liczba jedności ma bowiem postać \(5 + n\), gdzie n jest liczbą jedności mnożnika. Zaobserowane prawidłowości warto spróbować zrozumieć, pytając "dlaczego", ponieważ to właśnie "koincydencje" tego rodzaju są istotną treścią matematyki, a nie sama tylko tabliczka mnożenia. Zrozumienie nie jest sprawą łatwą i wymaga determinacji, na którą niekoniecznie stać sześcioletnie dziecko, które okazało się wystarczająco przenikliwe, żeby dostrzec ową dziwną zbieżność. Można próbować rozmaitych podpowiedzi, pamiętając wszakże, że radość samodzielnego odkrycia jest tym, co w rozumieniu świata jest najfajniejsze. Podpowiedź dla chcących podpowiedzieć dorosłych jest taka, że \(6 = 5 + 1\), więc \(6n = 5n + n\), a 5 jest połową dziesiątki, czyli podstawy systemu dziesiętnego. Pełny dowód twierdzenia sześcioletniej Marysi Wicher, które poznałem dzięki uprzejmości jej mamy, Barbary Świst-Wicher, jednej z aktywnych prekursorek edukacji domowej znajduje się tutaj.

Istnieje prawdopodobnie mnóstwo tego rodzaju symetrii i prawidłowości w tabliczce mnożenia i ich źródłem jest sama struktura dziesiętnego zapisu liczb, którego używamy i którego uczymy dzieci, często nie mając świadomości, że w istocie to właśnie robimy i że dla dzieci ten zapis ani nie jest naturalny, ani łatwo zrozumiały. Tu niżej proponuję obserwację dziwnych zachowań sum cyfr wyników mnożenia, ale możliwych jest z pewnością wiele innych tego typu zabaw.

Wszystkie one są czymś na kształt wnikliwej obserwacji cieni w platońskiej jaskini i próby odganięcia z nich istoty tych rzeczy, które owe cienie rzucają.

 

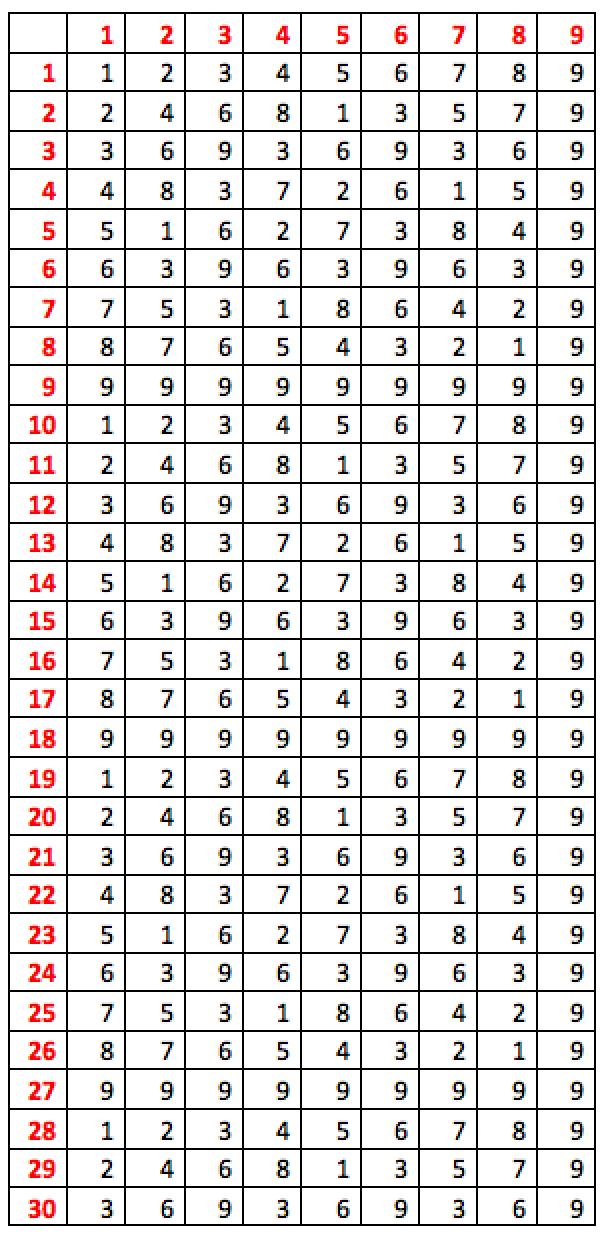
Przedstawiona obok tabela jest „dłuższa” niż zwykła tabliczka mnożenia, a przy tym zawiera nie same iloczyny liczb zaznaczonych na czerwono w nagłówkowym wierszu i kolumnie, ale ich pewną pochodną. Tabela podaje mianowicie „jednocyfrową sumę cyfr” iloczynu. Np. 9 x 11 = 99. Suma cyfr liczby 99 wynosi 18, jest więc sama dwucyfrowa – z kolei suma cyfr liczby 18 wynosi 9 i tę wartość tu wpisano. Jak widać, 9 jest jednocyfrową sumą dla wszystkich tu widocznych wielokrotności dziewiątki i w rzeczywistości dla wszystkich w ogóle.

Do pobrania tutaj – arkusz kalkulacyjny MS Excel z funkcjami liczącymi określone w ten sposób sumy cyfr. Jest ważne, żeby dzieci, widząc tę tabliczkę, wiedziały, jak wyglądają same iloczyny, zwykłe sumy cyfr i skąd się bierze „suma jednocyfrowa”, jednak zatrudnianie ich przy wypełnianiu tabelki – im większej, tym fajniej wyglądającej – jest niecelowo żmudne. Lepiej skorzystać z Excela. Sens miałoby natomiast zatrudnienie starszych dzieci, by załączone tu proste funkcje zaprogramowały samodzielnie.

Proszę spojrzeć na regularności, nierzadko skomplikowane, np. w kolumnie wielokrotności piątki, gdzie nieregularna sekwencja 9 różnych sum – 5, 1, 6, 2, 7, 3, 8, 4, 9 – powtarza się jednak stale. Dla szóstki sekwencja jest krótsza – 6, 3, 9 – i również się powtarza. Wielokrotności trójki dają inną sekwencję tych samych sum – 3, 6, 9. W każdej z tych kolumn i w każdym wierszu dzieje się coś regularnego i nieco dziwnego. Dlaczego tak się dzieje?

Otóż pytanie dlaczego, to jeden ze sposobów poznawania tabliczki mnożenia przez dzieci, które jej jeszcze nie znają i na pewno nie mają jej „opanowanej” na sposób szkolny. No, trzeba je tym zaciekawić – w kolejnej części materiału przykład sposobu na zaciekawienie, o ile nie wystarczy sama tajemnicza regularność, którą tu widzimy. Chodzi w każdym razie o to, by zamiast wbijać dzieciom do głowy pamięciowo opanowywane wyniki mnożeń, pokazać im raczej strukturę liczb i ich rozmaite, nierzadko głębokie symetrie. Zapamiętają, co im się zdarzy zapamiętać w trakcie poszukiwania zależności i ich wyjaśnień, ale nauczą się przy tym przede wszystkim na wiele sposobów dociekać wyjaśnień. Co ważniejsze, poznają jakiś rodzaj tej samej niedostępnej ograniczonym zmysłom rzeczywistości, o której opowiada Platon w historii o jaskini. Ta rzeczywistość ukrywa się bowiem w prostej, ale nieoczywistej strukturze. Jest to przy tym najzwyczajniej w świecie struktura układu dziesiętnego liczb, której w ogromnej większości głęboko nie rozumiemy, właśnie niemal jak ludzie w jaskini – choć posługujemy się nią codziennie.

Liczbami w pierwszej i ostatniej kolumnie rządzi ta sama reguła – w rzeczywistości ta sama reguła określa wszystkie widoczne tu prawidłowości. Przyjrzyjmy się niektórym – poczynając od trywialnych wielokrotności jedynki. Powtarzający się cykl dziewięciu kolejnych liczb wynika tu – jak widzimy – wprost z konstrukcji dziesiętnego zapisu. Widoczna z kolei obok kolumna wielokrotności dwójki zawiera oczywiście co drugą wartość z kolumny jedynek, a ponieważ cykl jedynek ma 9 elementów, co nie dzieli się przez 2, w kolumnie dwójek czteroelementowa sekwencja parzystych 2, 4, 6, 8 następuje naprzemiennie z pięcioelementową sekwencją liczb nieparzystych: 1, 3, 5, 7 i 9. W kolumnie wielokrotności trójek sytuacja się upraszcza, ponieważ 9 dzieli się na 3 i wobec tego wybierając co trzeci element, mamy 3, 6 i 9 powtarzające się stale. Dalej sytuacja komplikuje się zdecydowanie bardziej, co również warto byłoby prześledzić z dziećmi, choć utrzymanie ich uwagi bywa tu już trudne. Warto dlatego, że zachowanie dwóch nakładających się na siebie cykli określa wzajemna podzielność ich długości, podobne zjawiska rządzą np. rezonansem akustycznym, co może dać okazję do dygresji.

Wreszcie docieramy do dziewiątki, gdzie sytuacja jest oczywista, skoro wybieramy co dziewiąty element z listy jedynek. Dziesiątka powtarza jedynkę, jedenastka – dwójkę. By rzecz zrozumieć w pełni, warto spojrzeć na inną postać tego samego problemu.

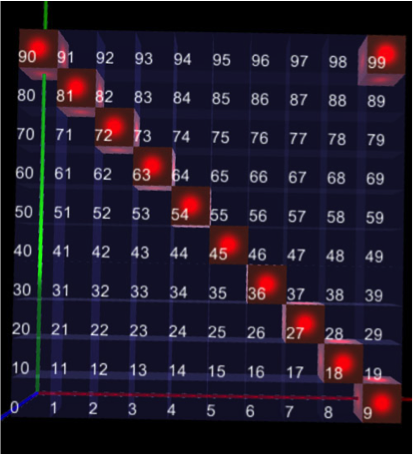
Wróćmy więc do układu znanego z poprzedniej części, a sytuacja stanie się całkiem jasna. Rysunek przedstawia kolejne wielokrotności dziewiątki zaznaczone na czerwono na płaszczyźnie pierwszych 100 liczb od 0 do 99. Widać tu kolejny sens zastosowania tego swoistego „układu współrzędnych”, który wykorzystaliśmy poprzednio z dziećmi dla dodawania. Otóż dodać dziewięć to tyle, co przesunąć się w górę o jeden wiersz dziesiątek i cofnąć o jedno pole wzdłuż „osi” jednostek. Jak widać, w większości wypadków dodawanie dziewiątki nie zmienia sumy cyfr. Same zaś wielokrotności dziewiątki leżą z jednym wyjątkiem na przekątnej kwadratu liczb, a ona ma to do siebie, że suma „współrzędnych” jest tu stała i wynosi 9. Wzdłuż tej przekątnej jedna ze współrzędnych rośnie, a druga maleje.

Ale widzimy także wyjątek, kiedy dochodzimy do ostatniej z widocznych wyżej liczb. 99. Suma 18. Nadal jest oczywiście podzielna przez 9, a jej „pochodzenie” staje się zrozumiałe. Suma cyfr zwiększa się o 9 przy przejściu przez 0 – zresztą na którymkolwiek miejscu dziesiętnego zapisu, a nie tylko na ostatnim. W kolejnych setkach liczb przekątne przesuwają się odpowiednio – jak to widać na kolejnych rysunkach.

W przedziale pomiędzy 200 i 299 dodawanie dziewiątki rozpoczyna się od siódemki – znów suma cyfr nie ulega zmianie, skoro nadal przechodzimy o jeden wiersz dziesiątek w górę, cofając się równocześnie o jednostkę. Do sumy brakuje kolejnej współrzędnej, reprezentowanej przez pierwszą liczbę zapisu – liczbę setek, których pionowa oś w użytym tu „układzie współrzędnych” jest na tym rysunku niewidoczna.

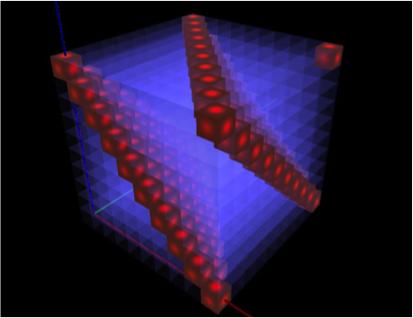
Zobaczmy przestrzenny obraz sytuacji. Przekątne, które w kolejnych setkach przesuwają się w stronę początku układu utworzą skośne płaszczyzny – jeśli setki ułożymy jedna na drugiej w sześcian. W widocznym tu zakresie od 0 do 999 zobaczymy – jak powinniśmy się tego spodziewać, obserwując setne przekroje – dwie takie płaszczyzny i zalążek trzeciej, która w kolejnych tysiącach – gdybyśmy je np. poukładali jeden nad drugim w słupek – byłaby kontynuowana równolegle do tej, która w tej chwili kończy się na linii przekątnej górnej ściany sześcianu. Ale kostek nie będziemy ustawiać na sobie, ponieważ nieco bardziej subtelna wizualizacja posłuży nam w kolejnej części do dalszych rozważań tropem Platona i Dalego. Zamiast tego zobaczymy kolejne tysiące jako specyficzne, trójwymiarowe przekroje czterowymiarowej przestrzeni. Obrazy -- również dla wielokrotności innych liczb -- da się wygenerować przy pomocy niewielkiej aplikacji dostępnej tu.

Podobnie, jak przesuwały się przekątne w kwadratach kolejnych setek, tak w kolejnych tysiącach identycznie przesuwają się skośne płaszczyzny:

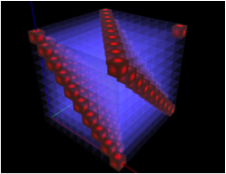
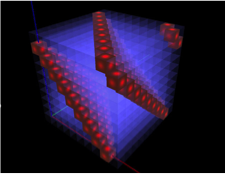
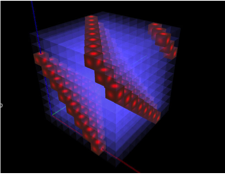
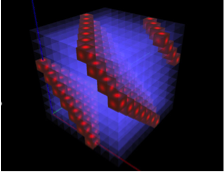
Wszystko to jest zrozumiałe, ale należy jeszcze w tych przestrzennych sytuacjach zrozumieć, w jaki sposób „dziesiętne współrzędne” wszystkich tych zaznaczonych tu wielokrotności dziewiątki dodają się do bardzo stałych sum również podzielnych przez dziewięć. Warto również zinterpretować fakt, że na wszystkich ścianach widocznych tu sześcianów sytuacja zmienia się tak samo i identycznie, jak zmieniały się linie w kolejnych setkach, ale również – zwróćmy uwagę – w dowolnie określonych przekrojach tak skonstruowanych sześcianów. Te obseracje i ich wyjaśnienia nie są już trywialne.

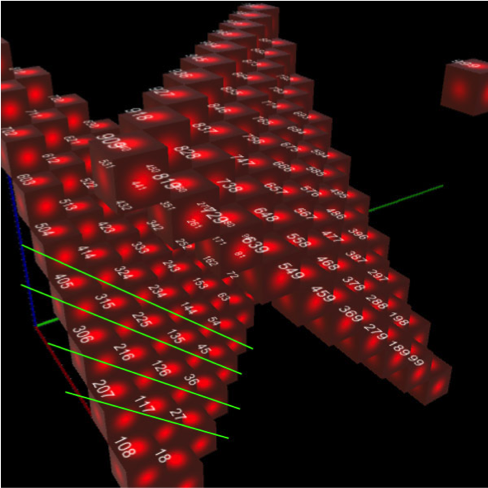
Kolejny rysunek pokazuje wielokrotności dziewiątek w pierwszym tysiącu liczb. Rozmaite symetrie da się na nim obserwować i wyjaśniać w nieskończoność. Tu widać jak wzdłuż zielonych linii leżą liczby, których dwie pierwsze cyfry sumują się tak, że dostajemy w efekcie 27 w pierwszej linii, 36 w drugiej itd.

Zjawiska tego rodzaju warto więc z dziećmi obserwować nie tylko w samej tabliczce mnożenia, ale również w innych układach, wśród których ten tutaj pokazywany („układ współrzędnych dziesiętnych”) wydaje się interesujący z kilku powodów – będzie wyglądał zaskakująco przy ułamkach dziesiętnych; będzie dostarczał dodatkowych intuicji arytmetycznych; sprzyja uogólnieniom i rozwijał zdolność przestrzennego myślenia, co będziemy eksploatować ekstremalnie intensywnie w ostatniej części materiału.

Pytań „dlaczego” dotyczących sytuacji pokazanych np. zielonymi liniami powyżej da się zadać bardzo wiele. Podobne obserwacje dotyczące wielokrotności dziewiątki i pozostałych liczb są trudne. To jest być może etap charakterystyczny dla kolejnego momentu z przytoczonego fragmentu Platona:

„Jak by to było, gdyby ktoś został wyzwolony lecz musiałby zaraz wstać i obrócić szyję, i iść, i patrzeć w światło. Czy nie cierpiałby robiąc to wszystko, a tak by mu w oczach migotało, że nie mógłby patrzeć na te rzeczy których cienie poprzednio oglądał? (…) A gdyby go ktoś zmuszał, żeby patrzał w samo światło, to bolałyby go oczy, odwracałby się i uciekał do tych rzeczy, na które potrafi patrzeć…”

Cóż, bywa, że zrozumienie wymaga wysiłku, następuje nie od razu i wywołuje reakcje obronne. Na tego rodzaju zajęcia można jednak poświęcić sporo czasu (np. większość matematyki w trzech latach nauczania początkowego), postępować powoli, darując sobie za to rozmaite ćwiczenia, a zwłaszcza pamięciowy trening tabliczki mnożenia. Analizę proponuję zacząć od dziewiątki, bo jest ciekawa, ma fajne zastosowanie, o którym w kolejnej części, a przy tym łatwo w niej zauważyć prawidłowości, które przy innych liczbach dodatkowo się komplikują. Kolejna powinna być jedenastka – podobnie symetryczna w przestrzennym układzie (odwrotne przekątne), a w tabliczce mnożenia pokazanej tu na początku ujawniająca te same własności, co kolumna wielokrotności dwójki. Dwunastka powtarza z kolei regularność trójki – czy dlatego, że sumy cyfr trójki i dwunastki są te same? Kontynuowanie obserwacji dla kolejnych liczb grozi schematyzmem, przed którym należy przestrzec, choć z drugiej strony przyniesie „opanowanie” tabliczki mnożenia na poziomie nieosiągalnym w „tradycyjny”, pamięciowy i bezmyślny sposób. Tabliczka mnożenia nie jest co prawda wartym uwagi „celem nauczania”, ale da się ją tą metodą pozbawić przynajmniej części ogłupiających efektów.

Narzędziem użytecznym w rozważaniu tych i innych problemów jest niewielki programik, z którego Czytelnicy (oraz uczniowie) mogą skorzystać online lub zainstalować na własnych komputerach. Przyda się z pewnością – to są bowiem rzeczy, w których wyobraźni potrzeba często wsparcia, a rysunki bywają trudne do wykonania. Niezależnie od tego jednak – warto z dziećmi próbować rysować i używać wyobraźni zamiast gotowych obrazów tak długo, jak to tylko jest możliwe. Obserwacje i rozumowania tu przedstawione są – sprawdzałem – całkowicie dla zrozumiałe dla dzieci z klas I – III, choć oczywiście najmłodsze maluchy mają kłopot z utrzymaniem potrzebnej tu uwagi. Grupa dzieci sprawdza się znakomicie w wynajdowaniu regularności, co udaje się dosyć łatwo, jeśli skorzystać choćby z takiej komputerowej kostki i pozwolić się nią pobawić dzieciom. Materiał jest w gruncie rzeczy rozszerzeniem typowych metod stosowanych w szkołach Montessori.

Poznaliśmy wyżej zarys dwóch dowodów faktu, że suma cyfr liczby podzielnej przez 9 jest również podzielna przez 9. Pierwszy z nich, przypomnijmy, polegał na obserwacji sumy cyfr kolejnych liczb naturalnych, na co nakłada się cykl, w którym w przypadku dziewiątki wybieramy co dziewiąty element. Cykle i ich obserwacja to zaś niebanalne zagadnienie z zakresu kombinatoryki. Warto pójść w tę stronę. Uzupełnienia wymaga w tym materiale np. dowód faktu, że maksymalna długość cyklu, w którym powtarzają się „jednocyfrowe sumy cyfr” w pierwszej z przytoczonych tu tabel, wynosi 9. Dowód „nie wprost” warto byłoby również przeanalizować z dziećmi, wprowadzając je przy okazji w zagadnienia arytmetyk modularnych. Przykłady i problemy z tym związane powinny zostać tu dołączone również.

Dowód drugi zawiera się w powyższych obserwacjach wielokrotności dziewiątki na płaszczyznach kolejnych setek i w trójwymiarowej przestrzeni. Widzimy, że dodanie 9 do dowolnej liczby, albo nie zmienia sumy cyfr, albo zmienia ją o wielokrotność dziewiątki. Trzeba by tu wziąć pod uwagę sytuacje w rodzaju 9999 + 9 = 10008 (suma cyfr maleje o 18) i sformalizować dowód do jakiejś eleganckiej postaci, ale jeśli istotnie pokazujemy te rzeczy i podobne rozumowania dzieciom w ramach nauczania początkowego, formalizmów należy się wystrzegać równie mocno, jak pamięciowych ćwiczeń. To jest zaś przykład typowego rozumowania indukcyjnego. Zasada sumy cyfr zgadza się oczywiście na początku – dla dziewiątki. Widzimy potem, że jeśli jakakolwiek liczba N ma sumę cyfr podzielną przez 9, to i liczba N + 9 musi mieć tę samą własność – z czego wynika prawdziwość naszej obserwacji dla wszystkich liczb. Na ten sposób rozumowania warto zwracać dzieciom uwagę.

Trzeci dowód tego samego faktu będzie miał już mniej więcej formalny charakter, a przy tym będzie stanowił ekstremalną lekcję algorytmów działań pisemnych. Do rozważenia pozostaje też dowód twierdzenia odwrotnego: że mianowicie każda liczba, której suma cyfr jest podzielna przez 9, dzieli się przez 9. Dowód nie jest skomplikowany, choć dla maluchów będzie prawdopodobnie trudny – no, wypada jednak dla porządku uzupełnić również to.

Zadania dla nauczycieli:

1. rozumieć powyższe;
2. ocenić przydatność, a jeśli ocena będzie pozytywna:
3. przygotować zestaw problemów związanych z rozpoznawaniem symetrii i wzorców w świecie liczb;
4. zaaranżować sytuacje, w których dzieci zadają sobie wzajemnie pytania o wyjaśnienie zauważonych cech symetrii;
5. umiejętnie odpowiadać na pytania dzieci;
6. sprowokować wyjaśnienia, dlaczego;
7. nie wymagać „opanowania materiału”;
8. zwracać uwagę na ogólność zagadnień, podkreślać zasady rozumowania.