Język dla każdego nauczanego przedmiotu jest bardzo ważny, ale szczególnie jest on istotny dla matematyki.
Używanie terminów – takich jak np. „nieparzysty” i „objętość” – może mieć różne znaczenia w różnych dziedzinach. Często matematyczny język nie jest dla uczniów intuicyjny. Weźmy np. pojęcie liczby pierwszej, definicja matematyczna nie ma nic wspólnego z intuicją, nawet więcej, liczba 1, którą wiele dzieci może uznać za pierwszą, nie jest przez matematyków uznana za pierwszą.
Autorka artykułu, z którego korzystam – Lanella Sweet, zbadała powiązanie u dzieci znaczenia intuicyjnego z formalnym, dla kilku pojęć matematycznych. Na przykład dzieci mówiły, że pojęcie „suma” można byłoby zastąpić – „dodaj” lub „ile jeszcze”.
Uczniowie badali i dyskutowali znaczenie słów, a następnie tworzyli ich własne rozumienie. Stwierdzono, że warto sięgać do intuicji i znaczenia nowo wprowadzanych terminów matematycznych.
Ważne było zrozumienie, w jaki sposób specyficzne słowa matematyczne odnoszą się zarówno do komunikacji przedmiotowej, jak i do codziennego użytku.
Pomocne może być polecenie opisania w małych grupach uczniowskich użycia określonych słów. Czyli tworzenia własnych definicji dla pojęć matematycznych.
Wielu uczniów rozwija i tworzy unikalne i znaczące powiązania z obszarem rzeczywistości i języka matematycznego. To angażuje uczniów w poznawanie pojęć matematycznych.
Dla uczniów starszych np. licealistów, również istotne jest „uwewnętrznienie” nowego pojęcia. Można zapytać uczniów, czy ich zdaniem możliwa byłaby bardziej adekwatna nazwa do danego terminu. Wiem z własnego doświadczenia, że uczniowie są bardzo kreatywni w podawaniu propozycji, a jednocześnie lepiej zaczynają rozumieć dane pojęcie.
Znaczenie pojęcia moim zdaniem jest kluczowe dla uczącego się matematyki. Z mojego doświadczenia wynika, że brak zrozumienia definicji uniemożliwia uczniowi nauczenie się matematyki.
Inspiracja artykułem Lanelli Sweet
Witold Szwajkowski, który od lat zajmuje się nauczaniem matematyki i właśnie znaczeniem pojęć matematycznych stworzył tekst, w którym pozmieniał nazwy pojęć. Bardzo polecam zapoznanie się z tekstem i poczucie, jak czuje się uczeń pierwszy raz słysząc pewne terminy.
Witold Szwajkowski
Test empatii dydaktycznej dla nauczycieli matematyki
Przeczytaj ze zrozumieniem poniższy tekst.
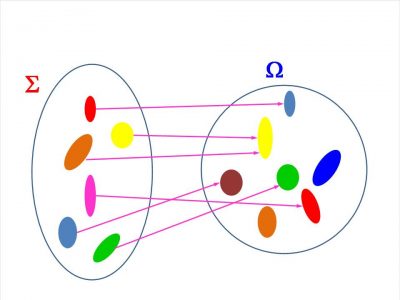
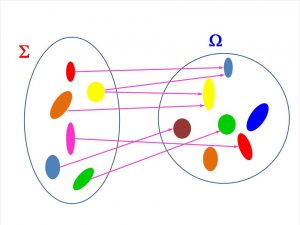
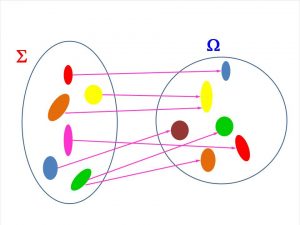
Weźmy dwie grupy S i W. Jeśli każdy obiekt grupy S skojarzymy z jednym i tylko jednym obiektem grupy W, to takie skojarzenie nazywamy możliwością od grupy S do grupy W.
Obiekty grupy S nazywamy wnioskami możliwości, a całą grupę S – obszarem możliwości. Obiekt grupy W, skojarzony z wnioskiem nazywamy gotowością możliwości dla tego wniosku. Wszystkie obiekty grupy W skojarzone z wnioskami nazywamy grupą gotowości możliwości, a całą grupę W – antyobszarem.
Zadanie
Znajdź rysunek ilustrujący możliwość od grupy S do grupy W. Jaki kolor ma na nim gotowość możliwości dla niebieskiego wniosku? Jakie kolory mają te obiekty antyobszaru, które nie wchodzą w skład grupy gotowości możliwości?
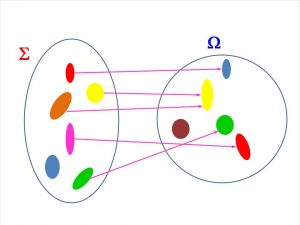
Jak poszło?
Co poczuje przeciętny, dorosły człowiek, który po przeczytaniu takiego wyjaśnienia miałby się zmierzyć z następującym po nim zadaniem? Mniej więcej to samo czuje prawdopodobnie przeciętny uczeń czytając opis bardzo ważnego pojęcia matematycznego – funkcji. Porównajmy opis ze wstępu z wyjaśnieniem pojęcia funkcji.
|
Weźmy dwie grupy S i W. Jeśli każdy obiekt grupy S skojarzymy z jednym i tylko jednym obiektem grupy W to takie skojarzenie nazywamy możliwością od grupy S do grupy W.
Obiekty grupy S nazywamy a całą grupę S – obszarem możliwości. Obiekt grupy W, skojarzony z wnioskiem nazywamy
Wszystkie obiekty grupy W skojarzone z wnioskami nazywamy grupą gotowości możliwości a całą grupę W – antyobszarem.
|
Weźmy dwa zbiory X i Y. Jeśli każdemu elementowi zbioru X przyporządkujemy jeden i tylko jeden element zbioru Y, to takie przyporządkowanie nazywamy funkcją ze zbioru X w zbiór Y.
Elementy zbioru X nazywamy a cały zbiór X – dziedziną funkcji. Element zbioru Y przyporządkowany argumentowi nazywamy wartością funkcji dla tego argumentu.
Wszystkie elementy zbioru Y przyporządkowane argumentom a cały zbiór Y – przeciwdziedziną.
|
Czy można się dziwić, że przeciętny uczeń po tego typu „wyjaśnieniu” traci wszelką ochotę na zgłębianie pojęcia funkcji oraz nadzieję, że cokolwiek z niego zrozumie i to przeważnie na całe życie? Szczególnie, gdy dojdą do tego wcześniejsze problemy z matematyką, mające często podobne, językowe źródło.
Zauważmy, że w obydwu opisach użyto słów, które same w sobie są trudne lub nie występują w znanych uczniom i ugruntowanych znaczeniach. Takim trudnym, niejednoznacznym słowem jest np. przyporządkowanie. Niełatwo je zrozumieć w oderwaniu od tego, co do czego przyporządkowujemy i w jakim celu, a kwestii celu akurat przy wprowadzeniu pojęcia funkcji zwykle się nie wyjaśnia. Jego odpowiednikiem w przedstawionym we wstępie opisie jest skojarzenie.
Samo słowo funkcja ma w języku potocznym zupełnie inne znaczenie niż w matematyce. Np. pan Kowalski pełni funkcję prezesa. Odpowiednikiem funkcji w przedstawionym opisie jest słowo możliwość. Słowo to, w swym podstawowym znaczeniu, jest również zupełnie niezwiązane z nowym nadanym mu w tym opisie znaczeniem. Czy łatwo je szybko zaakceptować w tej nowej roli?
Funkcja ma argumenty. Kolejne słowo znane uczniom w znaczeniu np. argumentów w dyskusji, a więc zupełnie nie związanym z nowym, matematycznym znaczeniem. W naszym opisie odpowiednikiem argumentów są wnioski. Czemu nie?
Zbiór argumentów to dziedzina funkcji. To kolejne znane dobrze słowo, w nowym dla ucznia znaczeniu, gdyż do tej pory kojarzył je np. z dziedziną nauki. W naszym opisie dziedzina to obszar, ale równie dobrze mogliśmy użyć jakiegoś innego rzeczownika, np. zakres.
Widać, że w przypadku wyjaśnienia pojęcia funkcji, nasycenie rzeczownikami użytymi w nowych znaczeniach i konieczność szybkiego operowania nimi może przekraczać granicę akceptowalną dla przeciętnego człowieka.
Ale to nie wszystko. Dowiadujemy się też, że funkcja przybiera jakąś wartość dla każdego argumentu. Z naszego opisu wynika, że możliwość przybiera gotowość dla każdego wniosku. Czemu nie? Jest to równie logiczne językowo! Ale zaraz, jeśli funkcja to przyporządkowanie, to jak przyporządkowanie może przybierać wartość? Gdy nieco się wgłębimy w sens pojęcia funkcji, to językowa nielogiczność będzie jeszcze bardziej widoczna: Jeśli np. w zbiorze X jest tylko jedno jabłko, a w zbiorze Y tylko jedna gruszka, to ta gruszka będzie wartością funkcji ze zbioru X w zbiór Y dla jabłka. Tak! Gruszka będzie wartością funkcji, czyli przyporządkowania dla jabłka! Wszystko jest zgodne z definicją, ale czy to jest jeszcze język polski?
W omawianym wyżej zdaniu pojawiły się przyimki: ze zbioru X w zbiór Y. Można zrozumieć, że rzeczowniki mogą mieć w danym języku zupełnie różne znaczenia, które odczytuje się z kontekstu. Jednak użycie przyimków w innych, kompletnie niezrozumiałych zbitkach niż te, które znamy z języka potocznego, wydaje się już być nadużyciem dokonanym na strukturze języka. Jaki sens, z uwagi na użyte przyimki, ma wyrażenie funkcja ze zbioru X w zbiór Y? Takie użycie przyimków raczej nie ma odpowiednika w języku polskim. Można byłoby powiedzieć: przyporządkowanie elementom zbioru X elementów ze zbioru Y, ale nie w zbiór Y! Poza tym, co to znaczy funkcja, czyli przyporządkowanie ze zbioru w zbiór? Użyte w naszym opisie określenie możliwość od grupy S do grupy W, brzmi zatem równie sensownie, a raczej równie bezsensownie.
Niestety, matematyka często nie radzi sobie z dobrym przetłumaczeniem wielu swoich pojęć na język polski, więc niech się nie dziwi, że trudno się z nią wielu ludziom porozumieć. Matematycy z pojęciem funkcji i towarzyszącą mu nomenklaturą są dobrze zaznajomieni
i oswojeni, więc nie rażą ich rzeczowniki użyte w innych niż podstawowe znaczeniach, ani nielogiczności językowe występujące w opisach, czy wyjaśnieniach.
Dlaczego jednak w podręcznikach dla dzieci, jeszcze nie matematyków i tych, którzy matematykami nigdy nie będą, kwestie potencjalnych trudności językowych nie są w ogóle brane pod uwagę? Dlaczego nie wyjaśnia się, że pojęcia funkcji (a także wielu innych: np. ułamka, pola, niewiadomej) uczniowie nie zrozumieją od razu, na podstawie definicji? Dlaczego nie uprzedza się ich, że muszą się z tym pojęciem stopniowo oswajać, poprzez przyzwyczajanie się nowych znaczeń słów, które wcześniej znali i zaakceptować także pewne językowe nielogiczności? Dlaczego nie buduje się przekonania, że nie ma w tym niczego złego ani niezwykłego, jeśli jakiś czas danego pojęcia nie będą rozumieli? Dlaczego atakuje się ich definicją, która dla wielu uczniów brzmi kompletnie niezrozumiale z wyjaśnionych wyżej powodów i doprowadza się ich w ten sposób do przekonania „chyba jestem za głupi, by to rozumieć. To nie dla mnie!”?
Czy to w porządku Pani Matematyko, by tak zrażać do siebie ludzi? Chyba, że zależy Ci na tym, aby w ten sposób szybko wyłowić tylko kandydatów do swojego elitarnego klubu, a cała reszta, pozbawiona praw do godnej edukacji, niech tam sobie żyje z poczuciem frustracji i wykluczenia.